Tekst je preuzet iz knjige Aha! Putovanje u središte problema Matije Bašića, izdavač HMD, 2020, uz dopuštenje autora.
Prvi i najjednostavniji princip koji koristimo je princip uzastopnog prebrojavanja. Koristimo ga u situacijama u kojima je bitan poredak objekata.
Primjer. Registarska oznaka se sastoji od tri dijela: prvi dio je oznaka grada, drugi je troznamenkasti broj, a treći dio se sastoji od dva slova. Na primjer: 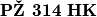 Broj gradova koji imaju svoju oznaku je
Broj gradova koji imaju svoju oznaku je 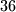 , znamenke mogu biti
, znamenke mogu biti 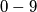 , a u hrvatskoj abecedi ima
, a u hrvatskoj abecedi ima  slova. Odredi broj različitih registarskih oznaka.
slova. Odredi broj različitih registarskih oznaka.
Rješenje. Kako bismo prebrojali sve registarske oznake, prebrojit ćemo na koliko načina možemo formirati jednu takvu oznaku. Oznaku grada možemo odabrati na 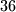 načina, troznamenkasti broj možemo odabrati na
načina, troznamenkasti broj možemo odabrati na 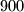 načina, a svako slovo možemo odabrati na
načina, a svako slovo možemo odabrati na  načina. Budući da moramo odabrati i oznaku gradu i troznamenkasti broj i dva slova traženi broj iznosi
načina. Budući da moramo odabrati i oznaku gradu i troznamenkasti broj i dva slova traženi broj iznosi 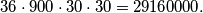
Uočite da smo broj troznamenkastih brojeva također mogli prebrojati koristeći princip uzastopnog prebrojavanja: prvu znamenku možemo odabrati na  načina (jer ta znamenka ne smije biti
načina (jer ta znamenka ne smije biti  ), a drugu i treću znamenku smo mogli odabrati svaku na
), a drugu i treću znamenku smo mogli odabrati svaku na  načina. Dakle, ukupan broj troznamenkastih brojeva je
načina. Dakle, ukupan broj troznamenkastih brojeva je 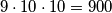 .
.
Rješenje zapisano u obliku 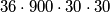 govori više o strukturi rješenja nego broj
govori više o strukturi rješenja nego broj 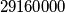 . Zato u kombinatornim zadacima najčešće nećemo računati koliko iznosi krajnje rješenje.
. Zato u kombinatornim zadacima najčešće nećemo računati koliko iznosi krajnje rješenje.
Objekte koji zadovoljavaju određene uvjete prebrojavamo tako da zamišljamo kako bismo korak po korak konstruirali proizvoljan takav objekt i u svakom koraku brojimo na koliko načina napraviti odabir.
Upišite 0 kao rješenje za prijelaz na sljedeći primjer.
Tekst je preuzet iz knjige \textit{Aha! Putovanje u središte problema} Matije Bašića, izdavač HMD, 2020, uz dopuštenje autora.
Prvi i najjednostavniji princip koji koristimo je \emph{princip uzastopnog prebrojavanja}. Koristimo ga u situacijama u kojima je bitan poredak objekata.
\textbf{Primjer.} Registarska oznaka se sastoji od tri dijela: prvi dio je oznaka grada, drugi je troznamenkasti broj, a treći dio se sastoji od dva slova. Na primjer:
$$\textbf{PŽ 314 HK}$$
Broj gradova koji imaju svoju oznaku je $36$, znamenke mogu biti $0-9$, a u hrvatskoj abecedi ima $30$ slova. Odredi broj različitih registarskih oznaka.
\textbf{Rješenje.} Kako bismo prebrojali sve registarske oznake, prebrojit ćemo na koliko načina možemo formirati jednu takvu oznaku. Oznaku grada možemo odabrati na $36$ načina, troznamenkasti broj možemo odabrati na $900$ načina, a svako slovo možemo odabrati na $30$ načina. Budući da moramo odabrati i oznaku gradu i troznamenkasti broj i dva slova traženi broj iznosi
$$36 \cdot 900 \cdot 30 \cdot 30 = 29160000.$$
Uočite da smo broj troznamenkastih brojeva također mogli prebrojati koristeći princip uzastopnog prebrojavanja: prvu znamenku možemo odabrati na $9$ načina (jer ta znamenka ne smije biti $0$), a drugu i treću znamenku smo mogli odabrati svaku na $10$ načina. Dakle, ukupan broj troznamenkastih brojeva je $9 \cdot 10 \cdot 10 = 900$.
Rješenje zapisano u obliku $36 \cdot 900 \cdot 30 \cdot 30$ govori više o strukturi rješenja nego broj $29160000$. Zato u kombinatornim zadacima najčešće nećemo računati koliko iznosi krajnje rješenje.
\textbf{Objekte koji zadovoljavaju određene uvjete prebrojavamo tako da zamišljamo kako bismo korak po korak konstruirali proizvoljan takav objekt i u svakom koraku brojimo na koliko načina napraviti odabir.}
\textit{Upišite 0 kao rješenje za prijelaz na sljedeći primjer.}
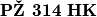 Broj gradova koji imaju svoju oznaku je
Broj gradova koji imaju svoju oznaku je 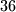 , znamenke mogu biti
, znamenke mogu biti 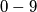 , a u hrvatskoj abecedi ima
, a u hrvatskoj abecedi ima  slova. Odredi broj različitih registarskih oznaka.
slova. Odredi broj različitih registarskih oznaka.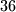 načina, troznamenkasti broj možemo odabrati na
načina, troznamenkasti broj možemo odabrati na 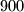 načina, a svako slovo možemo odabrati na
načina, a svako slovo možemo odabrati na  načina. Budući da moramo odabrati i oznaku gradu i troznamenkasti broj i dva slova traženi broj iznosi
načina. Budući da moramo odabrati i oznaku gradu i troznamenkasti broj i dva slova traženi broj iznosi 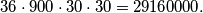
 načina (jer ta znamenka ne smije biti
načina (jer ta znamenka ne smije biti  ), a drugu i treću znamenku smo mogli odabrati svaku na
), a drugu i treću znamenku smo mogli odabrati svaku na  načina. Dakle, ukupan broj troznamenkastih brojeva je
načina. Dakle, ukupan broj troznamenkastih brojeva je 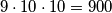 .
.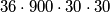 govori više o strukturi rješenja nego broj
govori više o strukturi rješenja nego broj 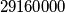 . Zato u kombinatornim zadacima najčešće nećemo računati koliko iznosi krajnje rješenje.
. Zato u kombinatornim zadacima najčešće nećemo računati koliko iznosi krajnje rješenje.