Faktorijeli
Prethodni primjer jako dobro ilustrira jedan od osnovnih načina razmišljanja koji koristimo kad rješavamo zadatke s prebrojavanjem. Pri prebrojavanju smo simulirali kako bismo na općeniti (generički) način konstruirali jedan objekt traženog tipa (registarsku oznaku). Taj objekt smo konstruirali tako da smo redom konstruirali manje dijelove tog objekta.
U zapisivanju rješenja koristimo oznaku za umnožak prvih  brojeva
brojeva 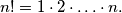
Izraz 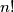 čitamo n faktorijel. Posebno definiramo da je
čitamo n faktorijel. Posebno definiramo da je 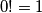 . Ta konvencija je odabrana jer uz nju vrijedi
. Ta konvencija je odabrana jer uz nju vrijedi

Primjer. Na koliko načina možemo rasporediti  knjiga iz matematike i
knjiga iz matematike i  iz fizike tako da knjige iz fizike budu sve zajedno?
iz fizike tako da knjige iz fizike budu sve zajedno?
Rješenje. Knjige iz fizike moraju biti zajedno, pa ih promatramo kao jedan blok. Kad god baratamo blokovima, potrebno je rasporediti objekte unutar bloka, te rasporediti blokove zajedno s drugim objektima. Pri tome svaki blok tretiramo kao zasebni objekt. Unutar bloka,  knjiga možemo rasporediti na
knjiga možemo rasporediti na 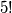 načina.
načina.
Jednom kad smo rasporedili knjige u bloku, taj blok doživljavamo kao jedan objekt koji razmještamo zajedno s  knjiga iz matematike. Ukupno trebamo rasporediti
knjiga iz matematike. Ukupno trebamo rasporediti  objekata, što možemo na
objekata, što možemo na 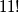 načina. Konačno rješenje je tada
načina. Konačno rješenje je tada 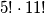 .
.
Upišite 0 kao rješenje za prijelaz na sljedeći primjer.
