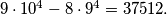Primjer. Koliko ima peteroznamenkastih brojeva koji sadrže znamenku  ?
?
Prvo rješenje. Zadatak možemo riješiti podjelom na slučajeve, no da ne bismo više puta brojali iste brojeve moramo sustavno brojati. Stoga razlikujemo na kojoj se poziciji znamenka  prvi put pojavljuje slijeva.
prvi put pojavljuje slijeva.
Ako je prva znamenka  , onda svaku od preostale četiri znamenke možemo odabrati na
, onda svaku od preostale četiri znamenke možemo odabrati na  načina, što daje
načina, što daje 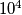 brojeva. Ako prva znamenka nije
brojeva. Ako prva znamenka nije  , onda ju možemo odabrati na
, onda ju možemo odabrati na  načina. Ako k tome druga znamenka iznosi
načina. Ako k tome druga znamenka iznosi  , onda preostale tri znamenke biramo na
, onda preostale tri znamenke biramo na 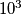 načina. U ovom slučaju imamo
načina. U ovom slučaju imamo 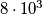 brojeva. Slično, ako se
brojeva. Slično, ako se  prvi put pojavljuje na trećem mjestu, onda prvu biramo na
prvi put pojavljuje na trećem mjestu, onda prvu biramo na  načina, drugu na
načina, drugu na  , a zadnje dvije na
, a zadnje dvije na 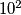 , što daje
, što daje 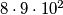 brojeva. Još nam preostaje dva slučaja, u kojima se
brojeva. Još nam preostaje dva slučaja, u kojima se  prvi put pojavljuje na četvrtom, odnosno petom mjestu. U tim slučajevima imamo
prvi put pojavljuje na četvrtom, odnosno petom mjestu. U tim slučajevima imamo 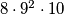 , odnosno
, odnosno 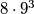 brojeva.
brojeva.
Na kraju, ukupan broj brojeva dobivamo zbrajanjem po svim slučajevima 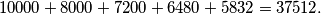 Ima ukupno
Ima ukupno 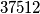 takvih brojeva.
takvih brojeva.
Drugo rješenje. Ukupan broj peteroznamenkastih brojeva je 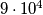 , svaki od njih ili sadrži ili ne sadrži znamenku
, svaki od njih ili sadrži ili ne sadrži znamenku  . Uočite da je mnogo jednostavnije prebrojati koliko ima peteroznamenkastih brojeva koji ne sadrže znamenku
. Uočite da je mnogo jednostavnije prebrojati koliko ima peteroznamenkastih brojeva koji ne sadrže znamenku  . Prvu znamenku možemo odabrati na
. Prvu znamenku možemo odabrati na  načina jer
načina jer  i
i  nisu dozvoljene znamenke, a sve ostale znamenke možemo odabrati na
nisu dozvoljene znamenke, a sve ostale znamenke možemo odabrati na  načina. Brojeva koji ne sadrže znamenku je
načina. Brojeva koji ne sadrže znamenku je 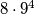 . Peteroznamenkastih brojeva koji sadrže znamenku
. Peteroznamenkastih brojeva koji sadrže znamenku  ima
ima 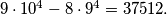
Prethodni primjer smo riješili na dva načina. U oba smo koristili podjelu na slučajeve. Vidimo da prvi način nije bio efikasan, dok smo u drugom iskoristili strategiju da pogledamo veću cjelinu od koje je traženi broj samo dio. Drugi način se svodi na prebrojavanje svih objekata koji nemaju traženo svojstvo iz veće cjeline i takav način razmišljanja nazivamo princip komplementa.
Upišite 0 kao rješenje za prijelaz na sljedeći primjer.
\textbf{Primjer.} Koliko ima peteroznamenkastih brojeva koji sadrže znamenku $3$?
\textbf{Prvo rješenje.} Zadatak možemo riješiti podjelom na slučajeve, no da ne bismo više puta brojali iste brojeve moramo sustavno brojati. Stoga razlikujemo na kojoj se poziciji znamenka $3$ prvi put pojavljuje slijeva.
Ako je prva znamenka $3$, onda svaku od preostale četiri znamenke možemo odabrati na $10$ načina, što daje $10^4$ brojeva. Ako prva znamenka nije $3$, onda ju možemo odabrati na $8$ načina. Ako k tome druga znamenka iznosi $3$, onda preostale tri znamenke biramo na $10^3$ načina. U ovom slučaju imamo $8 \cdot 10^3$ brojeva.
Slično, ako se $3$ prvi put pojavljuje na trećem mjestu, onda prvu biramo na $8$ načina, drugu na $9$, a zadnje dvije na $10^2$, što daje $8 \cdot 9 \cdot 10^2$ brojeva.
Još nam preostaje dva slučaja, u kojima se $3$ prvi put pojavljuje na četvrtom, odnosno petom mjestu. U tim slučajevima imamo $8 \cdot 9^2 \cdot 10$, odnosno $8 \cdot 9^3$ brojeva.
Na kraju, ukupan broj brojeva dobivamo zbrajanjem po svim slučajevima
$$10000 + 8000 + 7200 + 6480 + 5832 = 37512.$$
Ima ukupno $37512$ takvih brojeva.
\textbf{Drugo rješenje.} Ukupan broj peteroznamenkastih brojeva je $9 \cdot 10^4$, svaki od njih ili sadrži ili ne sadrži znamenku $3$. Uočite da je mnogo jednostavnije prebrojati koliko ima peteroznamenkastih brojeva koji ne sadrže znamenku $3$. Prvu znamenku možemo odabrati na $8$ načina jer $0$ i $3$ nisu dozvoljene znamenke, a sve ostale znamenke možemo odabrati na $9$ načina. Brojeva koji ne sadrže znamenku je $8 \cdot 9^4$. Peteroznamenkastih brojeva koji sadrže znamenku $3$ ima $9 \cdot 10^4 - 8 \cdot 9^4 = 37512.$
Prethodni primjer smo riješili na dva načina. U oba smo koristili podjelu na slučajeve. Vidimo da prvi način nije bio efikasan, dok smo u drugom iskoristili strategiju da pogledamo veću cjelinu od koje je traženi broj samo dio. Drugi način se svodi na prebrojavanje svih objekata koji nemaju traženo svojstvo iz veće cjeline i takav način razmišljanja nazivamo \textbf{princip komplementa}.
\textit{Upišite 0 kao rješenje za prijelaz na sljedeći primjer.}
 ?
? prvi put pojavljuje slijeva.
prvi put pojavljuje slijeva. , onda svaku od preostale četiri znamenke možemo odabrati na
, onda svaku od preostale četiri znamenke možemo odabrati na  načina, što daje
načina, što daje 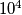 brojeva. Ako prva znamenka nije
brojeva. Ako prva znamenka nije  , onda ju možemo odabrati na
, onda ju možemo odabrati na  načina. Ako k tome druga znamenka iznosi
načina. Ako k tome druga znamenka iznosi  , onda preostale tri znamenke biramo na
, onda preostale tri znamenke biramo na 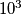 načina. U ovom slučaju imamo
načina. U ovom slučaju imamo 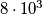 brojeva. Slično, ako se
brojeva. Slično, ako se  prvi put pojavljuje na trećem mjestu, onda prvu biramo na
prvi put pojavljuje na trećem mjestu, onda prvu biramo na  načina, drugu na
načina, drugu na  , a zadnje dvije na
, a zadnje dvije na 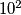 , što daje
, što daje 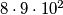 brojeva. Još nam preostaje dva slučaja, u kojima se
brojeva. Još nam preostaje dva slučaja, u kojima se  prvi put pojavljuje na četvrtom, odnosno petom mjestu. U tim slučajevima imamo
prvi put pojavljuje na četvrtom, odnosno petom mjestu. U tim slučajevima imamo 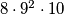 , odnosno
, odnosno 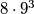 brojeva.
brojeva.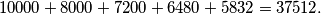 Ima ukupno
Ima ukupno 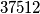 takvih brojeva.
takvih brojeva.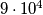 , svaki od njih ili sadrži ili ne sadrži znamenku
, svaki od njih ili sadrži ili ne sadrži znamenku  . Uočite da je mnogo jednostavnije prebrojati koliko ima peteroznamenkastih brojeva koji ne sadrže znamenku
. Uočite da je mnogo jednostavnije prebrojati koliko ima peteroznamenkastih brojeva koji ne sadrže znamenku  . Prvu znamenku možemo odabrati na
. Prvu znamenku možemo odabrati na  načina jer
načina jer  i
i  nisu dozvoljene znamenke, a sve ostale znamenke možemo odabrati na
nisu dozvoljene znamenke, a sve ostale znamenke možemo odabrati na  načina. Brojeva koji ne sadrže znamenku je
načina. Brojeva koji ne sadrže znamenku je 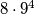 . Peteroznamenkastih brojeva koji sadrže znamenku
. Peteroznamenkastih brojeva koji sadrže znamenku  ima
ima