Princip uključivanja-isključivanja
Primjer. Koliko ima deveteroznamenkastih brojeva čije su znamenke 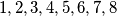 i
i  , a nikoje tri uzastopne znamenke nisu ni
, a nikoje tri uzastopne znamenke nisu ni 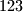 , ni
, ni 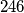 , ni
, ni 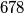 ?
?
Rješenje. Ukupno ima 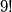 deveteroznamenkastih brojeva koji imaju znamenke od
deveteroznamenkastih brojeva koji imaju znamenke od  do
do  . Od toga broja moramo oduzeti broj brojeva koji imaju tri uzastopne znamenke
. Od toga broja moramo oduzeti broj brojeva koji imaju tri uzastopne znamenke 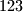 ,
, 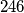 ili
ili 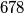 . Brojeva koji imaju uzastopne znamenke
. Brojeva koji imaju uzastopne znamenke 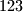 ima
ima 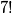 (permutiramo taj blok i preostalih
(permutiramo taj blok i preostalih  znamenaka). Analogno, brojeva koji sadrže
znamenaka). Analogno, brojeva koji sadrže 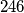 ima
ima 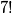 i brojeva koji sadrže
i brojeva koji sadrže 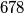 ima
ima 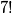 .
.
Uočimo da rješenje nije 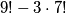 jer smo više puta oduzeli brojeve koji sadrže
jer smo više puta oduzeli brojeve koji sadrže 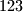 i
i 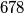 , odnosno one koji sadrže
, odnosno one koji sadrže 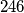 i
i 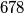 . Ne postoji broj kojemu su i
. Ne postoji broj kojemu su i 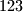 i
i 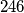 uzastopne znamenke.
uzastopne znamenke.
Brojeva koji sadrže 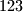 i
i 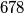 ima
ima 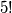 , a koji sadrže
, a koji sadrže 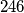 i
i 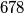 , tj.
, tj. 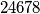 , ima također
, ima također 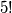 . Konačno rješenje je
. Konačno rješenje je 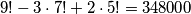 .
.
Ovdje smo koristili princip uključivanja-isključivanja u njegovom najjednostavnijem obliku. Vizualno možete predočiti skupove koje prebrojavamo Vennovim dijagramima.
Upišite 0 kao rješenje za prijelaz na sljedeći primjer.
