MetaMath '22 - demo

\textbf{Primjer.} U ravnini je dano $n$ točaka koje imaju svojstvo da svaki pravac određen s dvije dane točke prolazi barem još jednom danom točkom. Dokaži da sve točke leže na jednom pravcu. \textbf{Rješenje.} Promatramo samo brojeve 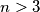$n > 3$, jer za manje $n$ tvrdnja trivijalno slijedi. Pretpostavimo suprotno, odnosno da ne leže sve točke na jednom pravcu. Ključna ideja u ovom zadatku je promotriti \emph{najmanju} pozitivnu udaljenost među svim točkama i pravaca određenih točkama. Neka je to udaljenost od točke $A$ do pravca $p$ koji prolazi točkama $B$ i $C$. Prema pretpostavci na pravcu $p$ se nalazi još jedna dana točka, nazovimo je $D$. Neka je $N$ nožište okomice iz $A$ na pravac $p$. Tada barem dvije od točaka $B$, $C$, $D$ leže na pravcu $p$ s iste strane točke $N$. Bez smanjenja općenitosti možemo pretpostaviti da su to $B$ i $C$, te da vrijedi $|CN|<|BN|$. 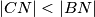Tada je točka $C$ bliža pravcu $AB$ nego točka $A$ pravcu $BC$ - označimo li s $M$ i $P$ redom nožišta okomica iz $C$ i $N$ na $AB$, onda je $|CM|<|NP|<|AN|$. 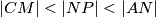Time smo dobili kontradikciju s izborom točke $A$ i pravca $p$, što pokazuje da je početna pretpostavka pogrešna. Dakle, sve dane točke moraju ležati na jednom pravcu. \textit{Upišite 0 kao rješenje za prijelaz na zadatke.}