Primjer. Na koliko načina u razredu od 30 ljudi možemo odabrati četvero predstavnika za školski kviz?
Rješenje. Kad bismo birali četiri predstavnika kojima se zna poredak, onda bi prema principu uzastopnog prebrojavanja to mogli učiniti na 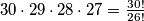 načina. No, budući da poredak nije važan, možemo među svim mogućim poretcima četiri osobe grupirati one poretke koji su sastavljeni od istih osoba. Broj različitih poredaka unutar jedne grupe je
načina. No, budući da poredak nije važan, možemo među svim mogućim poretcima četiri osobe grupirati one poretke koji su sastavljeni od istih osoba. Broj različitih poredaka unutar jedne grupe je 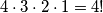 (opet, prema principu o uzastopnom prebrojavanju). Svaka grupa ima
(opet, prema principu o uzastopnom prebrojavanju). Svaka grupa ima 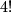 poredaka, a jedna grupa predstavlja točno izbor od četiri različite osobe, što želimo prebrojati. Zato je broj grupa, pa i traženi broj, jednak
poredaka, a jedna grupa predstavlja točno izbor od četiri različite osobe, što želimo prebrojati. Zato je broj grupa, pa i traženi broj, jednak 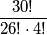 .
.
Općenito, ako želimo od  različitih objekata odabrati
različitih objekata odabrati  objekata, pri čemu nije važan njihov poredak, to možemo na
objekata, pri čemu nije važan njihov poredak, to možemo na 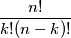 načina. Broj
načina. Broj 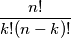 označavamo
označavamo 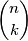 i zovemo binomni koeficijent. Više o binomnim koeficijentima možete pročitati u udžbeniku za 4. razred gimnazije, knjizi Aha! Putovanje u središte problema ili u drugim izvorima.
i zovemo binomni koeficijent. Više o binomnim koeficijentima možete pročitati u udžbeniku za 4. razred gimnazije, knjizi Aha! Putovanje u središte problema ili u drugim izvorima.
Sad ste spremni sami rješavati zadatke prebrojavanja!
Upišite 0 kao rješenje.
\textbf{Primjer.} Na koliko načina u razredu od 30 ljudi možemo odabrati četvero predstavnika za školski kviz?
\textbf{Rješenje.} Kad bismo birali četiri predstavnika kojima se zna poredak, onda bi prema principu uzastopnog prebrojavanja to mogli učiniti na $30\cdot 29 \cdot 28 \cdot 27 = \frac{30!}{26!}$ načina. No, budući da poredak nije važan, možemo među svim mogućim poretcima četiri osobe grupirati one poretke koji su sastavljeni od istih osoba. Broj različitih poredaka unutar jedne grupe je $4\cdot 3\cdot 2 \cdot 1=4!$ (opet, prema principu o uzastopnom prebrojavanju). Svaka grupa ima $4!$ poredaka, a jedna grupa predstavlja točno izbor od četiri različite osobe, što želimo prebrojati. Zato je broj grupa, pa i traženi broj, jednak $\displaystyle \frac{30!}{26!\cdot 4!}$.
Općenito, ako želimo od $n$ različitih objekata odabrati $k$ objekata, pri čemu nije važan njihov poredak, to možemo na $ \displaystyle\frac{n!}{k!(n-k)!}$ načina. Broj $\displaystyle \frac{n!}{k!(n-k)!}$ označavamo $\displaystyle {n \choose k}$ i zovemo \textbf{binomni koeficijent}. Više o binomnim koeficijentima možete pročitati u udžbeniku za 4. razred gimnazije, knjizi Aha! Putovanje u središte problema ili u drugim izvorima.
\textbf{Sad ste spremni sami rješavati zadatke prebrojavanja!}
\textit{Upišite 0 kao rješenje.}
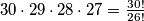 načina. No, budući da poredak nije važan, možemo među svim mogućim poretcima četiri osobe grupirati one poretke koji su sastavljeni od istih osoba. Broj različitih poredaka unutar jedne grupe je
načina. No, budući da poredak nije važan, možemo među svim mogućim poretcima četiri osobe grupirati one poretke koji su sastavljeni od istih osoba. Broj različitih poredaka unutar jedne grupe je 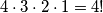 (opet, prema principu o uzastopnom prebrojavanju). Svaka grupa ima
(opet, prema principu o uzastopnom prebrojavanju). Svaka grupa ima 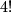 poredaka, a jedna grupa predstavlja točno izbor od četiri različite osobe, što želimo prebrojati. Zato je broj grupa, pa i traženi broj, jednak
poredaka, a jedna grupa predstavlja točno izbor od četiri različite osobe, što želimo prebrojati. Zato je broj grupa, pa i traženi broj, jednak 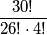 .
. različitih objekata odabrati
različitih objekata odabrati  objekata, pri čemu nije važan njihov poredak, to možemo na
objekata, pri čemu nije važan njihov poredak, to možemo na 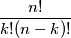 načina. Broj
načina. Broj 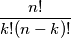 označavamo
označavamo 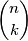 i zovemo binomni koeficijent. Više o binomnim koeficijentima možete pročitati u udžbeniku za 4. razred gimnazije, knjizi Aha! Putovanje u središte problema ili u drugim izvorima.
i zovemo binomni koeficijent. Više o binomnim koeficijentima možete pročitati u udžbeniku za 4. razred gimnazije, knjizi Aha! Putovanje u središte problema ili u drugim izvorima.