MetaMath '22 - demo

\textbf{Primjer.} Pod dimenzija 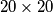$20 \times 20$ popločan je pločicama dimenzija 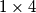$1\times 4$. Ako se jedna pločica razbije, možemo li presložiti pločice tako da ostane rupa koju možemo pokriti pločicom dimenzija 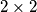$2\times 2$? \textbf{Rješenje.} Odgovor je ne. Kako bismo to pokazali, \emph{obojit} ćemo polja crno i bijelo na poseban način. Obojimo u svakom drugom retku svako drugo polje u crno. Tada svaka pločica dimenzija 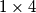$1\times 4$ pokriva nula ili dva crna polja, a pločica dimenzija 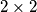$2\times 2$ pokriva uvijek točno jedno crno polje. Drugim riječima, pločica 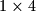$1 \times 4$ uvijek pokriva parno mnogo crnih polja, a pločica 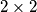$2 \times 2$ uvijek prekriva neparno mnogo crnih polja. Kada bismo mogli presložiti pločice 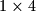$1 \times 4$ tako da ostane rupa dimenzija 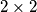$2\times 2$ i prekrijemo li nju pločicom 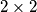$2 \times 2$, zaključujemo da pločice ukupno prekirivaju neparno mnogo crnih polja. No, prekrivena je cijela ploča na kojoj je parno mnogo crnih polja pa smo došli do kontradikcije i naša pretpostavka je pogrešna, odnosno nije moguće presložiti pločice na traženi način. U sljedećim zadacima potrebno je također odabirati razna bojanja ploče s ciljem dolaska u kontradikciju s nekim zahtjevima. Više primjera možete naći u online predavanju udruge MNM "Marin Getaldić" \url{https://www.skoljka.org/media/attachment/1/00109_yx1s73zdn0us54u88otp/Bojanja_i_poplocavanja.pdf}. \textit{Upišite 0 kao rješenje za prijelaz na zadatke.}