Primjer. Na školskoj ploči je napisano pet brojeva. U svakom koraku radimo sljedeću transformaciju: odabiremo bilo koja tri broja, nazovimo ih  ,
,  i
i  i mijenjamo ih u
i mijenjamo ih u 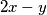 ,
, 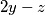 i
i 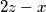 . Ako su na početku bili napisani brojevi
. Ako su na početku bili napisani brojevi 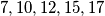 , možemo li, uzastopnim ponavljanjem tog postupka, doći do petorke brojeva: a)
, možemo li, uzastopnim ponavljanjem tog postupka, doći do petorke brojeva: a) 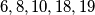 ? b)
? b) 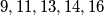 ?
?
Rješenje. U oba dijela ćemo uočiti veličinu koja se ne mijenja (tzv. invarijantu), te zaključiti budući da je iznos te veličine različit na početku i na kraju da nije moguće doći do željene petorke.
U a) dijelu će ta veličina biti broj parnih brojeva u petorki. Uočimo da je parnost brojeva  ,
,  i
i  jednaka redom parnosti brojeva
jednaka redom parnosti brojeva 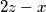 ,
, 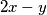 i
i 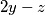 . To pokazuje da se broj parnih brojeva ne može promijeniti. Na početku, u petorci
. To pokazuje da se broj parnih brojeva ne može promijeniti. Na početku, u petorci 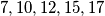 imamo točno dva parna broja, a u petorci
imamo točno dva parna broja, a u petorci 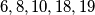 imamo četiri parna broja, pa tu petorku nije moguće postići.
imamo četiri parna broja, pa tu petorku nije moguće postići.
Za b) dio promatramo veličinu zbroj svih brojeva u petorki. Budući da je 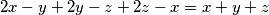 , uočavamo zaista da se zbroj brojeva u petorki ne mijenja primjenom dopuštene transformacije. Na početku, zbroj brojeva
, uočavamo zaista da se zbroj brojeva u petorki ne mijenja primjenom dopuštene transformacije. Na početku, zbroj brojeva 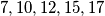 iznosi
iznosi 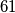 , a u petorci
, a u petorci 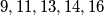 iznosi
iznosi 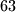 . Budući da je
. Budući da je 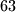 različito od
različito od 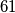 , ne možemo postići petorku
, ne možemo postići petorku 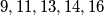 .
.
Uočite dodatno da je u zadatku namješteno tako da argument koji je dobar za jedan dio nije dobar za drugi. Naime, u petorci 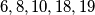 je zbroj
je zbroj 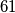 , a u petorci
, a u petorci 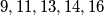 su točno dva broja parna. To pokazuje i da morate biti oprezni da činite logičku pogrešku. Bilo bi pogrešno nakon a) dijela rješenja reći "drugu petorku možemo postići jer ima dva parna broja".
su točno dva broja parna. To pokazuje i da morate biti oprezni da činite logičku pogrešku. Bilo bi pogrešno nakon a) dijela rješenja reći "drugu petorku možemo postići jer ima dva parna broja".
Više primjera možete naći na online predavanju udruge MNM "Marin Getaldić": https://www.skoljka.org/media/attachment/1/00104_lvzr5puzv9ueoe8rf6pw/invarijante.pdf.
Upišite 0 kao rješenje za prijelaz na sljedeći primjer.
\textbf{Primjer.} Na školskoj ploči je napisano pet brojeva. U svakom koraku radimo sljedeću transformaciju: odabiremo bilo koja tri broja, nazovimo ih $x$, $y$ i $z$ i mijenjamo ih u $2x-y$, $2y-z$ i $2z-x$. Ako su na početku bili napisani brojevi $7, 10, 12, 15, 17$, možemo li, uzastopnim ponavljanjem tog postupka, doći do petorke brojeva:
a) $6,8,10,18,19$?
b) $9,11,13,14,16$?
\textbf{Rješenje.} U oba dijela ćemo uočiti \emph{veličinu koja se ne mijenja} (tzv. \emph{invarijantu}), te zaključiti budući da je iznos te veličine različit na početku i na kraju da nije moguće doći do željene petorke.
U a) dijelu će ta veličina biti \textbf{broj parnih brojeva u petorki}. Uočimo da je parnost brojeva $x$, $y$ i $z$ jednaka redom parnosti brojeva $2z-x$, $2x-y$ i $2y-z$. To pokazuje da se broj parnih brojeva ne može promijeniti. Na početku, u petorci $7, 10, 12, 15, 17$ imamo točno dva parna broja, a u petorci $6,8,10,18,19$ imamo četiri parna broja, pa tu petorku nije moguće postići.
Za b) dio promatramo veličinu \textbf{zbroj svih brojeva u petorki}. Budući da je $2x-y+2y-z+2z-x=x+y+z$, uočavamo zaista da se zbroj brojeva u petorki ne mijenja primjenom dopuštene transformacije. Na početku, zbroj brojeva $7, 10, 12, 15, 17$ iznosi $61$, a u petorci $9,11,13,14,16$ iznosi $63$. Budući da je $63$ različito od $61$, ne možemo postići petorku $9,11,13,14,16$.
Uočite dodatno da je u zadatku namješteno tako da argument koji je dobar za jedan dio nije dobar za drugi. Naime, u petorci $6,8,10,18,19$ je zbroj $61$, a u petorci $9,11,13,14,16$ su točno dva broja parna. To pokazuje i da morate biti oprezni da činite logičku pogrešku. Bilo bi pogrešno nakon a) dijela rješenja reći "drugu petorku možemo postići jer ima dva parna broja".
Više primjera možete naći na online predavanju udruge MNM "Marin Getaldić": \url{https://www.skoljka.org/media/attachment/1/00104_lvzr5puzv9ueoe8rf6pw/invarijante.pdf}.
\textit{Upišite 0 kao rješenje za prijelaz na sljedeći primjer.}
 ,
,  i
i  i mijenjamo ih u
i mijenjamo ih u 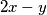 ,
, 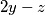 i
i 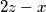 . Ako su na početku bili napisani brojevi
. Ako su na početku bili napisani brojevi 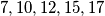 , možemo li, uzastopnim ponavljanjem tog postupka, doći do petorke brojeva: a)
, možemo li, uzastopnim ponavljanjem tog postupka, doći do petorke brojeva: a) 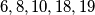 ? b)
? b) 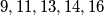 ?
? ,
,  i
i  jednaka redom parnosti brojeva
jednaka redom parnosti brojeva 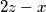 ,
, 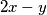 i
i 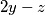 . To pokazuje da se broj parnih brojeva ne može promijeniti. Na početku, u petorci
. To pokazuje da se broj parnih brojeva ne može promijeniti. Na početku, u petorci 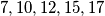 imamo točno dva parna broja, a u petorci
imamo točno dva parna broja, a u petorci 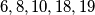 imamo četiri parna broja, pa tu petorku nije moguće postići.
imamo četiri parna broja, pa tu petorku nije moguće postići.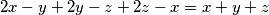 , uočavamo zaista da se zbroj brojeva u petorki ne mijenja primjenom dopuštene transformacije. Na početku, zbroj brojeva
, uočavamo zaista da se zbroj brojeva u petorki ne mijenja primjenom dopuštene transformacije. Na početku, zbroj brojeva 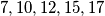 iznosi
iznosi 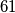 , a u petorci
, a u petorci 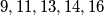 iznosi
iznosi 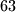 . Budući da je
. Budući da je 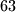 različito od
različito od 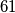 , ne možemo postići petorku
, ne možemo postići petorku 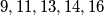 .
.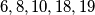 je zbroj
je zbroj 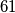 , a u petorci
, a u petorci 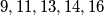 su točno dva broja parna. To pokazuje i da morate biti oprezni da činite logičku pogrešku. Bilo bi pogrešno nakon a) dijela rješenja reći "drugu petorku možemo postići jer ima dva parna broja".
su točno dva broja parna. To pokazuje i da morate biti oprezni da činite logičku pogrešku. Bilo bi pogrešno nakon a) dijela rješenja reći "drugu petorku možemo postići jer ima dva parna broja".