S obzirom da je umnožak u svakom retku i stupcu  , jasno je da u svakom retku i stupcu možemo imati točno jedno pojavljivanje broja s apsolutnom vrijednošću
, jasno je da u svakom retku i stupcu možemo imati točno jedno pojavljivanje broja s apsolutnom vrijednošću  . Broj načina na koje možemo odabrati polja na kojima će se nalaziti te brojke je
. Broj načina na koje možemo odabrati polja na kojima će se nalaziti te brojke je 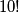 . Naime, u prvom retku možemo odabrati bilo koji od
. Naime, u prvom retku možemo odabrati bilo koji od  stupaca, u drugom retku potom bilo koji od
stupaca, u drugom retku potom bilo koji od  stupaca različitih od stupca odabranog u prvom retku, u trećem retku bilo koji od
stupaca različitih od stupca odabranog u prvom retku, u trećem retku bilo koji od  stupaca različitih od dvaju već odabranih stupaca, itd.
stupaca različitih od dvaju već odabranih stupaca, itd.
Nadalje, na svako od odabranih polja u prvih  redaka možemo postaviti ili
redaka možemo postaviti ili  ili
ili  što je
što je 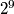 različitih odabira. U svakom od prvih
različitih odabira. U svakom od prvih  redaka sada imamo
redaka sada imamo  polja u koje moramo upisati vrijednosti
polja u koje moramo upisati vrijednosti  ili
ili  . Primijetimo da, s obzirom da je umnožak brojki u svakom retku jednak
. Primijetimo da, s obzirom da je umnožak brojki u svakom retku jednak  , kada upišemo vrijednosti na
, kada upišemo vrijednosti na  od tih
od tih  polja, preostalo polje je jedinstveno određeno. Stoga, za svaki od tih
polja, preostalo polje je jedinstveno određeno. Stoga, za svaki od tih  imamo
imamo 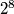 različitih odabira brojki
različitih odabira brojki  i
i  , tj ukupno
, tj ukupno 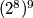 odabira.
odabira.
Sada smo u situaciji da su brojke napisane u sva polja u prvih  redaka i svi retci zadovoljavaju da je umnožak brojki u njima upravo
redaka i svi retci zadovoljavaju da je umnožak brojki u njima upravo  . Promotrimo sada prvih
. Promotrimo sada prvih  stupaca. Kako umnožak u svakom od njih mora biti
stupaca. Kako umnožak u svakom od njih mora biti  , jedinstveno su određene brojke koje moraju pisati u posljednjem retku tih stupaca. Promotrimo sada polje
, jedinstveno su određene brojke koje moraju pisati u posljednjem retku tih stupaca. Promotrimo sada polje 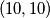 . Ondje moramo paziti na umnožak i po retku i po stupcu, a kako su sve brojke ondje već upisano, imamo na
. Ondje moramo paziti na umnožak i po retku i po stupcu, a kako su sve brojke ondje već upisano, imamo na  načina jedinstveno određenu brojku koja mora pisati u tom polju. Stoga, moramo pokazati da nam je potrebna jednaka brojka za postići umnožak
načina jedinstveno određenu brojku koja mora pisati u tom polju. Stoga, moramo pokazati da nam je potrebna jednaka brojka za postići umnožak  u
u 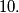 retku i u
retku i u 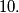 stupcu.
stupcu.
Neka je  umnožak svih brojki koje se nalaze i u prvih
umnožak svih brojki koje se nalaze i u prvih  redaka i u prvih
redaka i u prvih  stupaca,
stupaca,  umnožak brojki u prvih
umnožak brojki u prvih  redaka zadnjeg stupca,
redaka zadnjeg stupca,  umnožak brojki u prvih
umnožak brojki u prvih  stupaca zadnjeg retka te
stupaca zadnjeg retka te  brojka na polju
brojka na polju 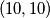 . Jasno je da vrijedi:
. Jasno je da vrijedi: 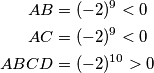
Iz prve  jednakosti zaključujemo da su
jednakosti zaključujemo da su  i
i  istog predznaka. Zato je
istog predznaka. Zato je  pozitivan pa je i
pozitivan pa je i  pozitivan, odnosno
pozitivan, odnosno  i
i  su istog predznaka. Dakle, predznak od
su istog predznaka. Dakle, predznak od  je jedinstveno određen predznakom od
je jedinstveno određen predznakom od  te je apsolutna vrijednost od
te je apsolutna vrijednost od  određena na početku, odabirom stupaca koji sadržavaju
određena na početku, odabirom stupaca koji sadržavaju  ili
ili  u svakom retku. Dakle, svaki od prebrojanih odabira brojeva je zaista ispravan.
u svakom retku. Dakle, svaki od prebrojanih odabira brojeva je zaista ispravan.
Stoga, konačno rješenje je 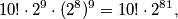 odabira, te je rješenje zadatka
odabira, te je rješenje zadatka 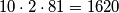 .
.
S obzirom da je umnožak u svakom retku i stupcu $-2$, jasno je da u svakom retku i stupcu možemo imati točno jedno pojavljivanje broja s apsolutnom vrijednošću $2$. Broj načina na koje možemo odabrati polja na kojima će se nalaziti te brojke je $10!$. Naime, u prvom retku možemo odabrati bilo koji od $10$ stupaca, u drugom retku potom bilo koji od $9$ stupaca različitih od stupca odabranog u prvom retku, u trećem retku bilo koji od $8$ stupaca različitih od dvaju već odabranih stupaca, itd.
Nadalje, na svako od odabranih polja u prvih $9$ redaka možemo postaviti ili $2$ ili $-2$ što je $2^9$ različitih odabira. U svakom od prvih $9$ redaka sada imamo $9$ polja u koje moramo upisati vrijednosti $1$ ili $-1$. Primijetimo da, s obzirom da je umnožak brojki u svakom retku jednak $-2$, kada upišemo vrijednosti na $8$ od tih $9$ polja, preostalo polje je jedinstveno određeno. Stoga, za svaki od tih $9$ imamo $2^8$ različitih odabira brojki $-1$ i $1$, tj ukupno $(2^8)^9$ odabira.
Sada smo u situaciji da su brojke napisane u sva polja u prvih $9$ redaka i svi retci zadovoljavaju da je umnožak brojki u njima upravo $-2$. Promotrimo sada prvih $9$ stupaca. Kako umnožak u svakom od njih mora biti $-2$, jedinstveno su određene brojke koje moraju pisati u posljednjem retku tih stupaca. Promotrimo sada polje $(10,10)$. Ondje moramo paziti na umnožak i po retku i po stupcu, a kako su sve brojke ondje već upisano, imamo na $2$ načina jedinstveno određenu brojku koja mora pisati u tom polju. Stoga, moramo pokazati da nam je potrebna jednaka brojka za postići umnožak $-2$ u $10.$ retku i u $10.$ stupcu.
Neka je $A$ umnožak svih brojki koje se nalaze i u prvih $9$ redaka i u prvih $9$ stupaca, $B$ umnožak brojki u prvih $9$ redaka zadnjeg stupca, $C$ umnožak brojki u prvih $9$ stupaca zadnjeg retka te $D$ brojka na polju $(10,10)$. Jasno je da vrijedi:
\begin{align*}
AB &= (-2)^9 < 0 \\
AC &= (-2)^9 < 0 \\
ABCD &= (-2)^{10} > 0
\end{align*}
Iz prve $2$ jednakosti zaključujemo da su $B$ i $C$ istog predznaka. Zato je $BC$ pozitivan pa je i $AD$ pozitivan, odnosno $A$ i $D$ su istog predznaka. Dakle, predznak od $D$ je jedinstveno određen predznakom od $A$ te je apsolutna vrijednost od $D$ određena na početku, odabirom stupaca koji sadržavaju $2$ ili $-2$ u svakom retku. Dakle, svaki od prebrojanih odabira brojeva je zaista ispravan.
Stoga, konačno rješenje je
$$10! \cdot 2^9 \cdot (2^8)^9 = 10! \cdot 2^{81},$$
odabira, te je rješenje zadatka $10 \cdot 2 \cdot 81 = 1620$.
 , jasno je da u svakom retku i stupcu možemo imati točno jedno pojavljivanje broja s apsolutnom vrijednošću
, jasno je da u svakom retku i stupcu možemo imati točno jedno pojavljivanje broja s apsolutnom vrijednošću  . Broj načina na koje možemo odabrati polja na kojima će se nalaziti te brojke je
. Broj načina na koje možemo odabrati polja na kojima će se nalaziti te brojke je 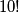 . Naime, u prvom retku možemo odabrati bilo koji od
. Naime, u prvom retku možemo odabrati bilo koji od  stupaca, u drugom retku potom bilo koji od
stupaca, u drugom retku potom bilo koji od  stupaca različitih od stupca odabranog u prvom retku, u trećem retku bilo koji od
stupaca različitih od stupca odabranog u prvom retku, u trećem retku bilo koji od  stupaca različitih od dvaju već odabranih stupaca, itd.
stupaca različitih od dvaju već odabranih stupaca, itd. redaka možemo postaviti ili
redaka možemo postaviti ili  ili
ili  što je
što je 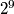 različitih odabira. U svakom od prvih
različitih odabira. U svakom od prvih  redaka sada imamo
redaka sada imamo  polja u koje moramo upisati vrijednosti
polja u koje moramo upisati vrijednosti  ili
ili  . Primijetimo da, s obzirom da je umnožak brojki u svakom retku jednak
. Primijetimo da, s obzirom da je umnožak brojki u svakom retku jednak  , kada upišemo vrijednosti na
, kada upišemo vrijednosti na  od tih
od tih  polja, preostalo polje je jedinstveno određeno. Stoga, za svaki od tih
polja, preostalo polje je jedinstveno određeno. Stoga, za svaki od tih  imamo
imamo 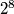 različitih odabira brojki
različitih odabira brojki  i
i  , tj ukupno
, tj ukupno 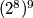 odabira.
odabira. redaka i svi retci zadovoljavaju da je umnožak brojki u njima upravo
redaka i svi retci zadovoljavaju da je umnožak brojki u njima upravo  . Promotrimo sada prvih
. Promotrimo sada prvih  stupaca. Kako umnožak u svakom od njih mora biti
stupaca. Kako umnožak u svakom od njih mora biti  , jedinstveno su određene brojke koje moraju pisati u posljednjem retku tih stupaca. Promotrimo sada polje
, jedinstveno su određene brojke koje moraju pisati u posljednjem retku tih stupaca. Promotrimo sada polje 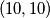 . Ondje moramo paziti na umnožak i po retku i po stupcu, a kako su sve brojke ondje već upisano, imamo na
. Ondje moramo paziti na umnožak i po retku i po stupcu, a kako su sve brojke ondje već upisano, imamo na  načina jedinstveno određenu brojku koja mora pisati u tom polju. Stoga, moramo pokazati da nam je potrebna jednaka brojka za postići umnožak
načina jedinstveno određenu brojku koja mora pisati u tom polju. Stoga, moramo pokazati da nam je potrebna jednaka brojka za postići umnožak  u
u 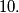 retku i u
retku i u 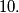 stupcu.
stupcu. umnožak svih brojki koje se nalaze i u prvih
umnožak svih brojki koje se nalaze i u prvih  redaka i u prvih
redaka i u prvih  stupaca,
stupaca,  umnožak brojki u prvih
umnožak brojki u prvih  redaka zadnjeg stupca,
redaka zadnjeg stupca,  umnožak brojki u prvih
umnožak brojki u prvih  stupaca zadnjeg retka te
stupaca zadnjeg retka te  brojka na polju
brojka na polju 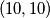 . Jasno je da vrijedi:
. Jasno je da vrijedi: 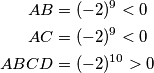
 jednakosti zaključujemo da su
jednakosti zaključujemo da su  i
i  istog predznaka. Zato je
istog predznaka. Zato je  pozitivan pa je i
pozitivan pa je i  pozitivan, odnosno
pozitivan, odnosno  i
i  su istog predznaka. Dakle, predznak od
su istog predznaka. Dakle, predznak od  je jedinstveno određen predznakom od
je jedinstveno određen predznakom od  te je apsolutna vrijednost od
te je apsolutna vrijednost od  određena na početku, odabirom stupaca koji sadržavaju
određena na početku, odabirom stupaca koji sadržavaju  ili
ili  u svakom retku. Dakle, svaki od prebrojanih odabira brojeva je zaista ispravan.
u svakom retku. Dakle, svaki od prebrojanih odabira brojeva je zaista ispravan.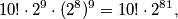 odabira, te je rješenje zadatka
odabira, te je rješenje zadatka 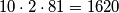 .
. 