MetaMath '22 - demo

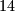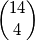Budući da svi putnici preferiraju sjediti sami, znamo da će postojati $10$ osoba koje sjede same, dok će preostalih $8$ osoba činiti $4$ para. Dakle. biramo $4$ među $14$ parova sjedala gdje će se nalaziti $2$ osobe, a to možemo učiniti na $\displaystyle {14 \choose 4}$ načina. Zatim, raspoređujemo točno $8$ osoba na mjesta na kojima sjede parovi. 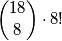To možemo učiniti na $\displaystyle {18 \choose 8} \cdot 8!$ načina. Množimo sa 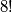$8!$ jer nam je bitno kako smo rasporedili odabranih $8$ osoba po sjedalima. Naposlijetku, raspoređujemo preostalih $10$ osoba koje sjede samostalno. 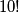Na $10!$ načina možemo odabrati koja osoba sjedi na kojem paru sjedala. To moramo pomnožiti sa 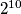$2^{10}$ jer svaka od osoba može sjediti na jednom od $2$ sjedala u paru. Stoga, konačan broj je 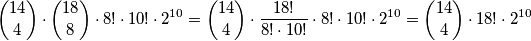$$\displaystyle {14 \choose 4} \cdot \displaystyle {18 \choose 8} \cdot 8! \cdot 10! \cdot 2^{10} = \displaystyle {14 \choose 4} \cdot \frac{18!}{8! \cdot 10!} \cdot 8! \cdot 10! \cdot 2^{10} = \displaystyle {14 \choose 4} \cdot 18! 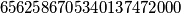\cdot 2^{10} $$ pa je rješenje zadatka $6562586705340137472000$.