Prebrojavanja: Sladoledi - RJEŠENJE
 sladoleda možemo rasporediti na
sladoleda možemo rasporediti na  osobe ili tako da
osobe ili tako da  osobe dobiju po
osobe dobiju po  sladoled te
sladoled te  osoba dobije
osoba dobije  sladoleda, ili tako da
sladoleda, ili tako da  osobe dobiju
osobe dobiju  sladoleda, a preostale
sladoleda, a preostale  po
po  sladoled.
sladoled.
U prvom slučaju, na 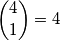 načina možemo odabrati koja osoba će dobiti
načina možemo odabrati koja osoba će dobiti  sladoleda, a zatim na
sladoleda, a zatim na 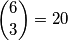 načina možemo odabrati koja
načina možemo odabrati koja  sladoleda dobiva ta osoba. Preostala
sladoleda dobiva ta osoba. Preostala  sladoleda ostalim trima osobama možemo podijeliti na
sladoleda ostalim trima osobama možemo podijeliti na 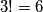 načina (prvoj osobi bilo koji od njih
načina (prvoj osobi bilo koji od njih  , drugoj bilo koji od preostala
, drugoj bilo koji od preostala  i zadnjoj osobi jedini preostali). To je ukupno
i zadnjoj osobi jedini preostali). To je ukupno 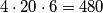 načina u ovom slučaju.
načina u ovom slučaju.
U drugom slučaju, na 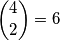 načina možemo izabrati koje
načina možemo izabrati koje  osobe će dobiti po
osobe će dobiti po  sladoleda. Zatim, na
sladoleda. Zatim, na 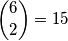 načina biramo
načina biramo  sladoleda među njih
sladoleda među njih  koja idu prvoj od dvije odabrane osobe, zatim na
koja idu prvoj od dvije odabrane osobe, zatim na 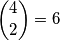 načina biramo
načina biramo  sladoleda od preostala
sladoleda od preostala  za drugu odabranu osobu. Naposljetku, na
za drugu odabranu osobu. Naposljetku, na  načina možemo dodijeliti zadnja
načina možemo dodijeliti zadnja  sladoleda preostalim dvjema osobama. To je ukupno
sladoleda preostalim dvjema osobama. To je ukupno 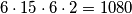 načina u ovom slučaju.
načina u ovom slučaju.
Stoga je konačno rješenje 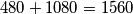 .
.
