MetaMath '22 - demo

Obojajmo ploču \textit{šahovski}, odnosno ako su retci numerirani 1-10 odozgo prema dolje, a stupci 1-10 slijeva nadesno, obojajmo polja čije koordinate su iste parnosti bijelom bojom, a preostala polja crnom bojom. Na ploči je tada $50$ crnih i $50$ bijelih polja. Primijetimo da uz predloženo bojanje vrijedi da svaka T-pločica pokriva ili $3$ crna ili $3$ bijela polja. Pretpostavimo sada da je ovakvo popločavanje moguće. 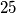Kako se ploča sastoji od $100$, a T-pločica od $4$ polja, iskoristili bismo $25$ T-pločica. Recimo da je $a$ pločica postavljeno tako da pokriva $3$ crna, a $b$ pločica tako da pokriva $3$ bijela polja. 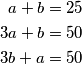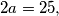Vrijede jednakosti \begin{align*} a + b &= 25 \\ 3a + b &= 50 \\ 3b + a &= 50 \end{align*} Izražavanjem $b$ preko $a$ iz prve jednadžbe i uvrštavanjem u drugu dobivamo $$2a = 25,$$ što je nemoguće s obzirom da su $a$ i $b$ cijeli brojevi. Dakle, naša pretpostavka je pogrešna i predloženo popločavanje je nemoguće.