U slučaju kada je  neparan, popločavanje je nemoguće jer se svaka L pločica sastoji od parno mnogo polja, a kada s ploče
neparan, popločavanje je nemoguće jer se svaka L pločica sastoji od parno mnogo polja, a kada s ploče  uklonimo
uklonimo  kutna polja, preostaje
kutna polja, preostaje 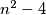 , odnosno neparan broj polja za popločati.
, odnosno neparan broj polja za popločati.
Preostaje pokazati da za  djeljiv s
djeljiv s  također ne možemo napraviti traženo popločavanje. Obojimo sva polja u neparnim retcima crnom bojom, a sva polja u parnim retcima bijelom bojom. Jasno je da na taj način dobivamo jednak broj bijelih i crnih polja na ploči. Primijetimo da bez obzira kako postavimo L pločicu, ona će uvijek pokrivati
također ne možemo napraviti traženo popločavanje. Obojimo sva polja u neparnim retcima crnom bojom, a sva polja u parnim retcima bijelom bojom. Jasno je da na taj način dobivamo jednak broj bijelih i crnih polja na ploči. Primijetimo da bez obzira kako postavimo L pločicu, ona će uvijek pokrivati  polja u jednoj boji te
polja u jednoj boji te  polje u drugoj boji. Pretpostavimo sada da smo uspjeli provesti željeno popločavanje i da smo to učinili s
polje u drugoj boji. Pretpostavimo sada da smo uspjeli provesti željeno popločavanje i da smo to učinili s  pločica koje pokrivaju
pločica koje pokrivaju  crna i
crna i  bijelo polje te s
bijelo polje te s  pločica koje pokrivaju
pločica koje pokrivaju  bijela i
bijela i  crno polje. Kako uklanjanjem kutnih polja preostaje
crno polje. Kako uklanjanjem kutnih polja preostaje 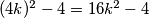 polja za popločavanje, vrijede jednakosti
polja za popločavanje, vrijede jednakosti 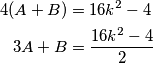 Naime, prva jednakost vrijedi jer svaka pločica pokriva točno
Naime, prva jednakost vrijedi jer svaka pločica pokriva točno  polja, a sa spomenutih
polja, a sa spomenutih 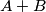 pločica smo uspjeli prekriti sva polja, dok druga jednakost vrijedi jer je točno polovica svih polja crna. Izrazimo li
pločica smo uspjeli prekriti sva polja, dok druga jednakost vrijedi jer je točno polovica svih polja crna. Izrazimo li  iz druge jednadžbe i uvrstimo li to u prvu jednadžbu, dobivamo
iz druge jednadžbe i uvrstimo li to u prvu jednadžbu, dobivamo 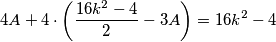 iz čega uz malo raspisivanja slijedi
iz čega uz malo raspisivanja slijedi 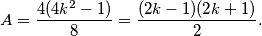 Time smo došli u kontradikciju, budući da
Time smo došli u kontradikciju, budući da  mora biti cijeli broj, a brojnik broja na desnoj strani je neparan. Dakle, naša pretpostavka je pogrešna i ovakvo popločavanje nije moguće.
mora biti cijeli broj, a brojnik broja na desnoj strani je neparan. Dakle, naša pretpostavka je pogrešna i ovakvo popločavanje nije moguće.
Primijetite da smo došli do kontradikcije na vrlo sličan način kao u zadatku s T pločicama. U oba slučaja smo odabrali bojanje upravo tako da pločice ne pokrivaju jednak broj crnih i bijelih polja i s tom asimetrijom smo uspjeli dolaziti do potrebnih kontradikcija.
U slučaju kada je $n$ neparan, popločavanje je nemoguće jer se svaka L pločica sastoji od parno mnogo polja, a kada s ploče $n \times n$ uklonimo $4$ kutna polja, preostaje $n^2-4$, odnosno neparan broj polja za popločati.
Preostaje pokazati da za $n$ djeljiv s $4$ također ne možemo napraviti traženo popločavanje. Obojimo sva polja u neparnim retcima crnom bojom, a sva polja u parnim retcima bijelom bojom. Jasno je da na taj način dobivamo jednak broj bijelih i crnih polja na ploči. Primijetimo da bez obzira kako postavimo L pločicu, ona će uvijek pokrivati $3$ polja u jednoj boji te $1$ polje u drugoj boji. Pretpostavimo sada da smo uspjeli provesti željeno popločavanje i da smo to učinili s $A$ pločica koje pokrivaju $3$ crna i $1$ bijelo polje te s $B$ pločica koje pokrivaju $3$ bijela i $1$ crno polje. Kako uklanjanjem kutnih polja preostaje $(4k)^2-4=16k^2-4$ polja za popločavanje, vrijede jednakosti
\begin{align*}
4(A+B) &= 16k^2-4 \\
3A + B &= \frac{16k^2-4}{2}
\end{align*}
Naime, prva jednakost vrijedi jer svaka pločica pokriva točno $4$ polja, a sa spomenutih $A+B$ pločica smo uspjeli prekriti sva polja, dok druga jednakost vrijedi jer je točno polovica svih polja crna. Izrazimo li $B$ iz druge jednadžbe i uvrstimo li to u prvu jednadžbu, dobivamo
$$4A + 4 \cdot \bigg( \frac{16k^2-4}{2} - 3A \bigg) = 16k^2-4$$
iz čega uz malo raspisivanja slijedi
$$A = \frac{4(4k^2-1)}{8} = \frac{(2k-1)(2k+1)}{2}.$$
Time smo došli u kontradikciju, budući da $A$ mora biti cijeli broj, a brojnik broja na desnoj strani je neparan. Dakle, naša pretpostavka je pogrešna i ovakvo popločavanje nije moguće.
Primijetite da smo došli do kontradikcije na vrlo sličan način kao u zadatku s T pločicama. U oba slučaja smo odabrali bojanje upravo tako da pločice ne pokrivaju jednak broj crnih i bijelih polja i s tom asimetrijom smo uspjeli dolaziti do potrebnih kontradikcija.
 neparan, popločavanje je nemoguće jer se svaka L pločica sastoji od parno mnogo polja, a kada s ploče
neparan, popločavanje je nemoguće jer se svaka L pločica sastoji od parno mnogo polja, a kada s ploče  uklonimo
uklonimo  kutna polja, preostaje
kutna polja, preostaje 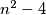 , odnosno neparan broj polja za popločati.
, odnosno neparan broj polja za popločati. djeljiv s
djeljiv s  također ne možemo napraviti traženo popločavanje. Obojimo sva polja u neparnim retcima crnom bojom, a sva polja u parnim retcima bijelom bojom. Jasno je da na taj način dobivamo jednak broj bijelih i crnih polja na ploči. Primijetimo da bez obzira kako postavimo L pločicu, ona će uvijek pokrivati
također ne možemo napraviti traženo popločavanje. Obojimo sva polja u neparnim retcima crnom bojom, a sva polja u parnim retcima bijelom bojom. Jasno je da na taj način dobivamo jednak broj bijelih i crnih polja na ploči. Primijetimo da bez obzira kako postavimo L pločicu, ona će uvijek pokrivati  polja u jednoj boji te
polja u jednoj boji te  polje u drugoj boji. Pretpostavimo sada da smo uspjeli provesti željeno popločavanje i da smo to učinili s
polje u drugoj boji. Pretpostavimo sada da smo uspjeli provesti željeno popločavanje i da smo to učinili s  pločica koje pokrivaju
pločica koje pokrivaju  crna i
crna i  bijelo polje te s
bijelo polje te s  pločica koje pokrivaju
pločica koje pokrivaju  bijela i
bijela i  crno polje. Kako uklanjanjem kutnih polja preostaje
crno polje. Kako uklanjanjem kutnih polja preostaje 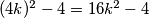 polja za popločavanje, vrijede jednakosti
polja za popločavanje, vrijede jednakosti 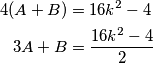 Naime, prva jednakost vrijedi jer svaka pločica pokriva točno
Naime, prva jednakost vrijedi jer svaka pločica pokriva točno  polja, a sa spomenutih
polja, a sa spomenutih 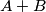 pločica smo uspjeli prekriti sva polja, dok druga jednakost vrijedi jer je točno polovica svih polja crna. Izrazimo li
pločica smo uspjeli prekriti sva polja, dok druga jednakost vrijedi jer je točno polovica svih polja crna. Izrazimo li  iz druge jednadžbe i uvrstimo li to u prvu jednadžbu, dobivamo
iz druge jednadžbe i uvrstimo li to u prvu jednadžbu, dobivamo 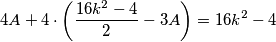 iz čega uz malo raspisivanja slijedi
iz čega uz malo raspisivanja slijedi 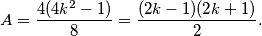 Time smo došli u kontradikciju, budući da
Time smo došli u kontradikciju, budući da  mora biti cijeli broj, a brojnik broja na desnoj strani je neparan. Dakle, naša pretpostavka je pogrešna i ovakvo popločavanje nije moguće.
mora biti cijeli broj, a brojnik broja na desnoj strani je neparan. Dakle, naša pretpostavka je pogrešna i ovakvo popločavanje nije moguće.