Odgovor je da je moguće dovesti sve žetone u jedan vrh ako i samo ako je  neparan.
neparan.
Kao i kod mnogih zadataka, i ovdje je najbolje krenuti s malim primjerima. U slučaju trokuta je vrlo jasno da izbor bilo koja  vrha odmah u prvom potezu rješava problem. U slučaju kvadrata, nakon kraćeg vremena pokušavanja naslućujemo da vjerojatno neće biti moguće postići željeni raspored žetona, jer se ponavlja nekoliko istih pozicija bez obzira na poteze koje isprobavamo.
vrha odmah u prvom potezu rješava problem. U slučaju kvadrata, nakon kraćeg vremena pokušavanja naslućujemo da vjerojatno neće biti moguće postići željeni raspored žetona, jer se ponavlja nekoliko istih pozicija bez obzira na poteze koje isprobavamo.
U slučaju peterokuta također nije pretjerano teško vidjeti da je moguć traženi niz poteza. Naime, označimo li vrhove redom od  do
do  u smjeru kazaljke na satu, lako se uvjerimo da niz poteza
u smjeru kazaljke na satu, lako se uvjerimo da niz poteza 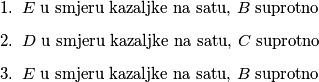 dovodi sve žetone u vrh
dovodi sve žetone u vrh  .
.
Iz toga možemo primijetiti i općeniti niz poteza koji će nas u slučaju neparnog 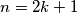 dovesti do željenog rasporeda žetona. Naime, kako imamo neparno mnogo vrhova, jednog možemo odabrati za "centralni" i promatrati kao da nam s njegove lijeve i desne strane ostaje po
dovesti do željenog rasporeda žetona. Naime, kako imamo neparno mnogo vrhova, jednog možemo odabrati za "centralni" i promatrati kao da nam s njegove lijeve i desne strane ostaje po  vrhova. Radimo nizove poteza u kojima biramo vrhove koji su jednako udaljeni od centralnog na lijevu i na desnu stranu te iz oba vrha približimo žeton za
vrhova. Radimo nizove poteza u kojima biramo vrhove koji su jednako udaljeni od centralnog na lijevu i na desnu stranu te iz oba vrha približimo žeton za  vrh bliže centralnom vrhu. Zbog simetrije ćemo konačnim nizom takvih poteza sve žetone slijeva i zdesna od centralnog vrha moći dovesti u njega.
vrh bliže centralnom vrhu. Zbog simetrije ćemo konačnim nizom takvih poteza sve žetone slijeva i zdesna od centralnog vrha moći dovesti u njega.
Nađimo sada invarijantu koja će dokazati da je nemoguće napraviti željeni niz poteza za parne  . Označimo vrhove mnogokuta redom brojevima od
. Označimo vrhove mnogokuta redom brojevima od  do
do  , u smjeru kazaljke na satu. Veličina koju ćemo promatrati je suma brojeva koje žetoni pokrivaju (brojimo svaki žeton, dakle neko polje više puta ako se na njemu nalazi više žetona). Primijetimo da u svakom potezu pomičemo jedan žeton u smjeru kazaljke na satu, a drugi u suprotnom smjeru što odgovara pomicanju jednog žetona na polje koje je za
, u smjeru kazaljke na satu. Veličina koju ćemo promatrati je suma brojeva koje žetoni pokrivaju (brojimo svaki žeton, dakle neko polje više puta ako se na njemu nalazi više žetona). Primijetimo da u svakom potezu pomičemo jedan žeton u smjeru kazaljke na satu, a drugi u suprotnom smjeru što odgovara pomicanju jednog žetona na polje koje je za  veće od prethodnog, a drugg žetona na polje koje je za
veće od prethodnog, a drugg žetona na polje koje je za  manje od prethodnog - osim u slučaju da imamo prebacivanje žetona između polja označenih s
manje od prethodnog - osim u slučaju da imamo prebacivanje žetona između polja označenih s  i
i  . Zato modificiramo veličinu koju promatramo i kao u brojnim ranijim zadacima i primjerima, promatrati ćemo ostatak koji spomenuta suma daje pri dijeljenju s
. Zato modificiramo veličinu koju promatramo i kao u brojnim ranijim zadacima i primjerima, promatrati ćemo ostatak koji spomenuta suma daje pri dijeljenju s  . Time smo riješili problem, s obzirom da je
. Time smo riješili problem, s obzirom da je 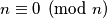 .
.
U slučaju parnog 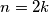 , na početku je vrijednost spomenute veličine
, na početku je vrijednost spomenute veličine 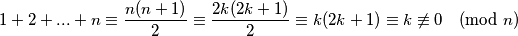 S druge strane, kada bismo doveli sve žetone u neko polje
S druge strane, kada bismo doveli sve žetone u neko polje  , vrijednost promatrane veličine bi bila
, vrijednost promatrane veličine bi bila 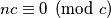 . Budući da smo pokazali da je promatrana veličina invarijantna pod dozvoljenim potezima, dobili smo kontradikciju i time je dokaz završen.
. Budući da smo pokazali da je promatrana veličina invarijantna pod dozvoljenim potezima, dobili smo kontradikciju i time je dokaz završen.
Odgovor je da je moguće dovesti sve žetone u jedan vrh ako i samo ako je $n$ neparan.
Kao i kod mnogih zadataka, i ovdje je najbolje krenuti s malim primjerima.
U slučaju trokuta je vrlo jasno da izbor bilo koja $2$ vrha odmah u prvom potezu rješava problem.
U slučaju kvadrata, nakon kraćeg vremena pokušavanja naslućujemo da vjerojatno neće biti moguće postići željeni raspored žetona, jer se ponavlja nekoliko istih pozicija bez obzira na poteze koje isprobavamo.
U slučaju peterokuta također nije pretjerano teško vidjeti da je moguć traženi niz poteza. Naime, označimo li vrhove redom od $A$ do $E$ u smjeru kazaljke na satu, lako se uvjerimo da niz poteza
\begin{enumerate}
\item{$E$ u smjeru kazaljke na satu, $B$ suprotno}
\item{$D$ u smjeru kazaljke na satu, $C$ suprotno}
\item{$E$ u smjeru kazaljke na satu, $B$ suprotno}
\end{enumerate}
dovodi sve žetone u vrh $A$.
Iz toga možemo primijetiti i općeniti niz poteza koji će nas u slučaju neparnog $n=2k+1$ dovesti do željenog rasporeda žetona. Naime, kako imamo neparno mnogo vrhova, jednog možemo odabrati za "centralni" i promatrati kao da nam s njegove lijeve i desne strane ostaje po $k$ vrhova. Radimo nizove poteza u kojima biramo vrhove koji su jednako udaljeni od centralnog na lijevu i na desnu stranu te iz oba vrha približimo žeton za $1$ vrh bliže centralnom vrhu. Zbog simetrije ćemo konačnim nizom takvih poteza sve žetone slijeva i zdesna od centralnog vrha moći dovesti u njega.
Nađimo sada invarijantu koja će dokazati da je nemoguće napraviti željeni niz poteza za parne $n$. Označimo vrhove mnogokuta redom brojevima od $1$ do $n$, u smjeru kazaljke na satu. Veličina koju ćemo promatrati je suma brojeva koje žetoni pokrivaju (brojimo svaki žeton, dakle neko polje više puta ako se na njemu nalazi više žetona). Primijetimo da u svakom potezu pomičemo jedan žeton u smjeru kazaljke na satu, a drugi u suprotnom smjeru što odgovara pomicanju jednog žetona na polje koje je za $1$ veće od prethodnog, a drugg žetona na polje koje je za $1$ manje od prethodnog - osim u slučaju da imamo prebacivanje žetona između polja označenih s $1$ i $n$. Zato modificiramo veličinu koju promatramo i kao u brojnim ranijim zadacima i primjerima, promatrati ćemo ostatak koji spomenuta suma daje pri dijeljenju s $n$. Time smo riješili problem, s obzirom da je $n \equiv 0 \pmod{n}$.
U slučaju parnog $n=2k$, na početku je vrijednost spomenute veličine
$$1 + 2 + ... + n \equiv \frac{n(n+1)}{2} \equiv \frac{2k(2k+1)}{2} \equiv k(2k+1) \equiv k \not\equiv 0 \pmod{n}$$
S druge strane, kada bismo doveli sve žetone u neko polje $c$, vrijednost promatrane veličine bi bila $nc \equiv 0 \pmod{c}$. Budući da smo pokazali da je promatrana veličina invarijantna pod dozvoljenim potezima, dobili smo kontradikciju i time je dokaz završen.
 neparan.
neparan. vrha odmah u prvom potezu rješava problem. U slučaju kvadrata, nakon kraćeg vremena pokušavanja naslućujemo da vjerojatno neće biti moguće postići željeni raspored žetona, jer se ponavlja nekoliko istih pozicija bez obzira na poteze koje isprobavamo.
vrha odmah u prvom potezu rješava problem. U slučaju kvadrata, nakon kraćeg vremena pokušavanja naslućujemo da vjerojatno neće biti moguće postići željeni raspored žetona, jer se ponavlja nekoliko istih pozicija bez obzira na poteze koje isprobavamo. do
do  u smjeru kazaljke na satu, lako se uvjerimo da niz poteza
u smjeru kazaljke na satu, lako se uvjerimo da niz poteza 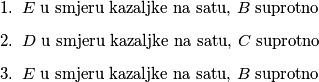 dovodi sve žetone u vrh
dovodi sve žetone u vrh  .
.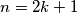 dovesti do željenog rasporeda žetona. Naime, kako imamo neparno mnogo vrhova, jednog možemo odabrati za "centralni" i promatrati kao da nam s njegove lijeve i desne strane ostaje po
dovesti do željenog rasporeda žetona. Naime, kako imamo neparno mnogo vrhova, jednog možemo odabrati za "centralni" i promatrati kao da nam s njegove lijeve i desne strane ostaje po  vrhova. Radimo nizove poteza u kojima biramo vrhove koji su jednako udaljeni od centralnog na lijevu i na desnu stranu te iz oba vrha približimo žeton za
vrhova. Radimo nizove poteza u kojima biramo vrhove koji su jednako udaljeni od centralnog na lijevu i na desnu stranu te iz oba vrha približimo žeton za  vrh bliže centralnom vrhu. Zbog simetrije ćemo konačnim nizom takvih poteza sve žetone slijeva i zdesna od centralnog vrha moći dovesti u njega.
vrh bliže centralnom vrhu. Zbog simetrije ćemo konačnim nizom takvih poteza sve žetone slijeva i zdesna od centralnog vrha moći dovesti u njega. . Označimo vrhove mnogokuta redom brojevima od
. Označimo vrhove mnogokuta redom brojevima od  do
do  , u smjeru kazaljke na satu. Veličina koju ćemo promatrati je suma brojeva koje žetoni pokrivaju (brojimo svaki žeton, dakle neko polje više puta ako se na njemu nalazi više žetona). Primijetimo da u svakom potezu pomičemo jedan žeton u smjeru kazaljke na satu, a drugi u suprotnom smjeru što odgovara pomicanju jednog žetona na polje koje je za
, u smjeru kazaljke na satu. Veličina koju ćemo promatrati je suma brojeva koje žetoni pokrivaju (brojimo svaki žeton, dakle neko polje više puta ako se na njemu nalazi više žetona). Primijetimo da u svakom potezu pomičemo jedan žeton u smjeru kazaljke na satu, a drugi u suprotnom smjeru što odgovara pomicanju jednog žetona na polje koje je za  veće od prethodnog, a drugg žetona na polje koje je za
veće od prethodnog, a drugg žetona na polje koje je za  manje od prethodnog - osim u slučaju da imamo prebacivanje žetona između polja označenih s
manje od prethodnog - osim u slučaju da imamo prebacivanje žetona između polja označenih s  i
i  . Zato modificiramo veličinu koju promatramo i kao u brojnim ranijim zadacima i primjerima, promatrati ćemo ostatak koji spomenuta suma daje pri dijeljenju s
. Zato modificiramo veličinu koju promatramo i kao u brojnim ranijim zadacima i primjerima, promatrati ćemo ostatak koji spomenuta suma daje pri dijeljenju s  . Time smo riješili problem, s obzirom da je
. Time smo riješili problem, s obzirom da je 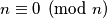 .
.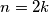 , na početku je vrijednost spomenute veličine
, na početku je vrijednost spomenute veličine 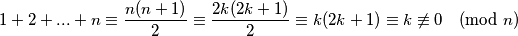 S druge strane, kada bismo doveli sve žetone u neko polje
S druge strane, kada bismo doveli sve žetone u neko polje  , vrijednost promatrane veličine bi bila
, vrijednost promatrane veličine bi bila 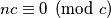 . Budući da smo pokazali da je promatrana veličina invarijantna pod dozvoljenim potezima, dobili smo kontradikciju i time je dokaz završen.
. Budući da smo pokazali da je promatrana veličina invarijantna pod dozvoljenim potezima, dobili smo kontradikciju i time je dokaz završen. 