MetaMath '22 - demo

Nejednakosti su jedna od najzastupljenijih grupa zadataka iz algebre na matematičkim natjecanjima. Općenito, u tim zadacima su zadana $2$ algebarska izraza koji se sastoje od jedne ili više varijabli i potrebno je dokazati da je jedan od tih izraza veći (ili jednak) od drugog izraza. Izraz je veći (ili jednak) od drugog izraza ako to vrijedi za sve dopuštene vrijednosti varijabli u tim izrazima. Samo dokazivanje provodi se svođenjem nejednakosti na neku očito istinitu ili poznatu nejednakost. Primjeri osnovnih nejednakosti su nenegativnost kvadrata realnih brojeva: 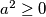$a^2 \geq 0$ za sve 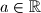$a \in \mathbb{R}$ te odnos umnoška i zbroja pozitivnih realnih brojeva: 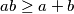$ab \ge a + b$ za sve 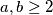$a, b \ge 2$ (dokažite formalno ovu nejednakost). Među poznate nejednakosti ubrajamo primjerice nejednakosti između brojevnih sredina i CSB nejednakost. Više o nejednakostima možete pronaći naravno u MNM predavanjima. \textbf{Primjer} Dokažite da za realne brojeve $a$ i $b$ vrijedi $a^2+b^2 \geq 2ab$. 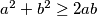\textbf{Rješenje} Prebacivanjem izraza 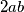$2ab$ na lijevu stranu nejednakosti dobivamo 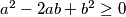$a^2-2ab+b^2 \geq 0$. Sada prepoznajemo da je izraz na lijevoj strani kvadrat razlike brojeva $a$ i $b$ pa smo zapravo došli do nejednakosti $(a-b)^2 \geq 0$. 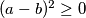Rekli smo da ova nejednakost vrijedi za bilo koji izbor realnih brojeva $a$ i $b$, a kako je ona \textit{ekvivalentna} početnoj nejednakosti, tj vrijedi ako i samo ako vijedi početna nejednakost, time smo dokazali i da je početna nejednakost istinita za svaki izbor brojeva $a$ i $b$. Kao rješenje, upišite koje godine je Cauchy objavio prvu verziju CSB nejednakosti.