Vrijeme: 01:56
Aritmetičke manipulacije - faktorizacija
Primjer
Neka su 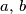 i
i  realni brojevi takvi da vrijedi
realni brojevi takvi da vrijedi 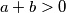 ,
, 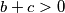 i
i 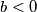 . Dokažite da vrijedi
. Dokažite da vrijedi 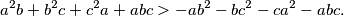
Rješenje
Prebacivanjem svih članova na istu stranu dobivamo 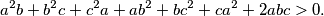 Izraz na lijevoj strani možemo faktorizirati grupirajući članove na sljedeći način
Izraz na lijevoj strani možemo faktorizirati grupirajući članove na sljedeći način 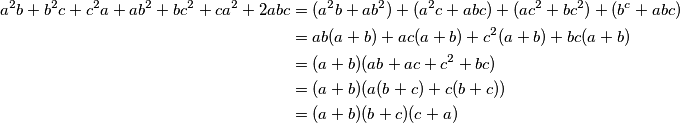 Dakle, dokažemo li da je
Dakle, dokažemo li da je 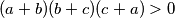 , biti će dokazana i početna nejednakost. Sada koristimo uvjete zadatka. Već znamo da je
, biti će dokazana i početna nejednakost. Sada koristimo uvjete zadatka. Već znamo da je 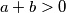 i
i 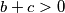 pa preostaje pokazati da je
pa preostaje pokazati da je 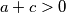 . Međutim, iz
. Međutim, iz 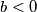 slijedi
slijedi 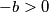 dok iz uvjeta
dok iz uvjeta 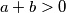 imamo
imamo 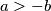 . Dakle,
. Dakle,  je pozitivan, a analogno dobivamo i da je
je pozitivan, a analogno dobivamo i da je  pozitivan pa je zaista i faktor
pozitivan pa je zaista i faktor 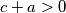 i tvrdnja je dokazana.
i tvrdnja je dokazana.
Kao rješenje, upišite za koliko je lijeva strana polazne nejednakosti veća od desne strane za 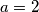 ,
, 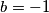 i
i 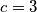 .
.
