MetaMath '22 - demo

Algebraske manipulacije i jednostavne nejednakosti mogu nam pomoći u mnogim problemima, ali kod nešto težih zadataka je potrebna malo "jača artiljerija". Pritom se misli na nejednakosti koje su posljedice zahtjevnijih matematičkih teorema, a mogu biti jako korisne u primjeni u zadacima s natjecanja. Daleko najkorištenija od takvih nejednakosti je \textbf{A-G nejednakost}, odnosno \textbf{aritmetičko-geometrijska nejednakost}. Njezina je tvrdnja da za pozitivne realne brojeve 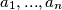$a_1,...,a_n$ vrijedi $$\frac{a_1+...+a_n}{n} \geq \sqrt[n]{a_1 \cdot ... \cdot a_n}.$$ Ova nejednakost može se koristiti u velikom broju raznolikih problema, počevši od najjednostavnijih od kojih smo neke već vidjeli pa do vrlo teških problema koje viđamo na državnim ili međunarodnim natjecanjima. \textbf{Primjer} Dokažite da za realne brojeve $a$ i $b$ vrijedi $a^2+b^2 \geq 2ab$. 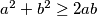\textbf{Rješenje} Već smo vidjeli rješenje ovog zadatka koristeći jednostavnije argumente. Ovdje ćemo pokazati da ga možemo riješiti i direktnom primjenom A-G nejednakosti. Naime, jednostavno je provjeriti da tvrdnja vrijedi ako je neki od brojeva $a$ i $b$ jednak $0$. 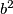U suprotnom, znamo da su $a^2$ i $b^2$ pozitivni realni brojevi pa možemo primijeniti A-G nejednakost i po njoj vrijedi $$\frac{a^2+b^2}{2} \geq \sqrt{a^2 \cdot b^2} = ab \hspace{1cm} \Rightarrow \hspace{1cm} a^2+b^2 \geq 2ab.$$ Često potpitanje u veće-ili-jednako nejednakostima jest kada se postiže jednakost izraza s lijeve i desne strane. Neka je vrijednost od $a$ u našem primjeru jednaka 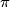$\pi$. Kao rješenje upišite vrijednost od $b$ za koju se u tom slučaju postiže jednakost. Zaključite kada se općenito postiže jednakost kod A-G nejednakosti.