A-G primjer 2
Primjer
Dokažite da za pozitivne realne brojeve 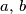 i
i  vrijedi
vrijedi 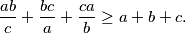
Rješenje
Probajmo kombinirati neka  ili možda čak sva
ili možda čak sva  člana na lijevoj strani kroz A-G nejednakost kako bismo na desnoj strani nejednakosti dobili
člana na lijevoj strani kroz A-G nejednakost kako bismo na desnoj strani nejednakosti dobili  . Ideja je onda analogni postupak primijeniti i na
. Ideja je onda analogni postupak primijeniti i na  i
i  i sumiranjem dobiti upravo promatranu nejednakost. Vidimo da izrazi
i sumiranjem dobiti upravo promatranu nejednakost. Vidimo da izrazi 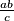 i
i 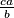 oba u brojniku imaju
oba u brojniku imaju  , dok se
, dok se  i
i  kod jednog izraza pojavljuju u brojniku, a kod drugog u nazivniku. To znači da ćemo u množenju koje se događa na desnoj strani A-G nejednakosti imati poništavanje članova
kod jednog izraza pojavljuju u brojniku, a kod drugog u nazivniku. To znači da ćemo u množenju koje se događa na desnoj strani A-G nejednakosti imati poništavanje članova  i
i  . To je motivacija za primjenu A-G nejednakosti na ova
. To je motivacija za primjenu A-G nejednakosti na ova  člana
člana 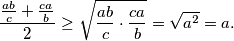 Sada analogno primijenjujemo na druga
Sada analogno primijenjujemo na druga  para pribrojnika na lijevoj strani početne nejednakosti i sumiranjem svih triju rezultata A-G nejednakosti je početna tvrdnja dokazana.
para pribrojnika na lijevoj strani početne nejednakosti i sumiranjem svih triju rezultata A-G nejednakosti je početna tvrdnja dokazana.
Kao rješenje upišite vrijednost od  i
i  za koju se postiže jednakost u slučaju
za koju se postiže jednakost u slučaju 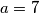 .
.
