Primjer
Za pozitivne realne brojeve 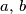 i
i  koji zadovoljavaju uvjet
koji zadovoljavaju uvjet 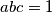 dokažite da vrijedi
dokažite da vrijedi 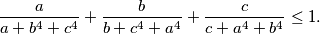
Rješenje
Promotrimo i jedan zahtjevniji primjer korištenja A-G nejednakosti na nešto drugačiji način od dosad. Prva stvar koju primjećujemo je da je znak nejednakosti  , a ne
, a ne  . Možemo se zapitati, pa kako iskoristiti A-G nejednakost na način da neki članovi s desne strane zadane nejednakosti budu veći ili jednaki nekim članovima na lijevoj strani nejednakosti kada se desno nalazi samo jedinica?
. Možemo se zapitati, pa kako iskoristiti A-G nejednakost na način da neki članovi s desne strane zadane nejednakosti budu veći ili jednaki nekim članovima na lijevoj strani nejednakosti kada se desno nalazi samo jedinica?
Odgovor je primjena A-G nejednakosti u nazivnicima izraza na lijevoj strani. Naime, ako koristeći A-G pokažemo primjerice da je nazivnik izraza 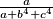 veći (ili jednak) od nekog
veći (ili jednak) od nekog  , onda će taj izraz zapravo biti manji (ili jednak) od
, onda će taj izraz zapravo biti manji (ili jednak) od 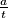 , što je smjer nejednakosti koji nam je potreban.
, što je smjer nejednakosti koji nam je potreban.
Druga stvar koju možemo primijetiti je nehomogenost, odnosno, nejednakost stupnjeva algebarskih izraza u nazivniku članova na lijevoj strani. Primjerice,  je stupnja
je stupnja  dok je
dok je 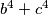 stupnja
stupnja  . Generalni princip je da je korisno imati homogen izraz jer nam to najčešće omogućuje smislenije primjene nejednakosti poput A-Ga i bolje faktorizacije. Način za postići homogenost je korištenje uvjeta zadatka. Imajmo to na umu jer ćemo u jednom trenutku rješenja htjeti provesti homogenizaciju u nazivniku.
. Generalni princip je da je korisno imati homogen izraz jer nam to najčešće omogućuje smislenije primjene nejednakosti poput A-Ga i bolje faktorizacije. Način za postići homogenost je korištenje uvjeta zadatka. Imajmo to na umu jer ćemo u jednom trenutku rješenja htjeti provesti homogenizaciju u nazivniku.
Primijenimo sada A-G nejednakost na sljedeći način ![b^4 + c^4 = \frac{b^4+b^4+b^4+c^4}{4} + \frac{b^4+c^4+c^4+c^4}{4} \geq \sqrt[4]{b^{12}c^4} + \sqrt[4]{b^4c^{12}} = b^3c + bc^3.](/media/m/8/8/1/881faa89e5d405c14042bc3c8f55138e.png) Tada za prvi izraz s lijeve strane početne nejednakosti vrijedi
Tada za prvi izraz s lijeve strane početne nejednakosti vrijedi 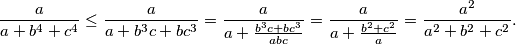 Pritom smo u drugoj jednakosti iskoristili uvjet zadatka, budući da je dijeljenje nečega s
Pritom smo u drugoj jednakosti iskoristili uvjet zadatka, budući da je dijeljenje nečega s 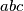 jednako kao da to dijelimo s
jednako kao da to dijelimo s  - dakle ne mijenja vrijednost izraza. Primjenom istog postupka na preostala dva izraza iz početne nejednakost i zbrajanjem dobivenih nejednakosti, slijedi tvrdnja zadatka.
- dakle ne mijenja vrijednost izraza. Primjenom istog postupka na preostala dva izraza iz početne nejednakost i zbrajanjem dobivenih nejednakosti, slijedi tvrdnja zadatka.
Ovo je teži zadatak. Ako ga niste sami uspjeli savladati, ne brinite. Važno je vidjeti i ovakve primjere i probati shvatiti motivaciju iza korištenih postupaka kako bi ih nakon nekog vremena i sami mogli primijenjivati. Uvjet zadatka i A-G su ovdje iskorišteni s motivacijom svođenja danih triju izraza na zajednički nazivnik - još jedan princip koji vrijedi imati na umu jer se nerijetko primjenjuje u zadacima s nejednakostima.
Ako ste spremni sami se okušati u zadacima s nejednakostima, upišite ,,DA'' kao rezultat!
\textbf{Primjer}
Za pozitivne realne brojeve $a, \, b$ i $c$ koji zadovoljavaju uvjet $abc=1$ dokažite da vrijedi
$$\frac{a}{a+b^4+c^4} + \frac{b}{b+c^4+a^4} + \frac{c}{c+a^4+b^4} \leq 1.$$
\textbf{Rješenje}
Promotrimo i jedan zahtjevniji primjer korištenja A-G nejednakosti na nešto drugačiji način od dosad. Prva stvar koju primjećujemo je da je znak nejednakosti $\leq$, a ne $\geq$. Možemo se zapitati, pa kako iskoristiti A-G nejednakost na način da neki članovi s desne strane zadane nejednakosti budu veći ili jednaki nekim članovima na lijevoj strani nejednakosti kada se desno nalazi samo jedinica?
Odgovor je primjena A-G nejednakosti u nazivnicima izraza na lijevoj strani. Naime, ako koristeći A-G pokažemo primjerice da je nazivnik izraza $\frac{a}{a+b^4+c^4}$ veći (ili jednak) od nekog $t$, onda će taj izraz zapravo biti manji (ili jednak) od $\frac{a}{t}$, što je smjer nejednakosti koji nam je potreban.
Druga stvar koju možemo primijetiti je \textit{nehomogenost}, odnosno, nejednakost \textit{stupnjeva} algebarskih izraza u nazivniku članova na lijevoj strani. Primjerice, $a$ je stupnja $1$ dok je $b^4+c^4$ stupnja $4$. Generalni princip je da je korisno imati homogen izraz jer nam to najčešće omogućuje smislenije primjene nejednakosti poput A-Ga i bolje faktorizacije. Način za postići homogenost je korištenje uvjeta zadatka. Imajmo to na umu jer ćemo u jednom trenutku rješenja htjeti provesti homogenizaciju u nazivniku.
Primijenimo sada A-G nejednakost na sljedeći način
$$b^4 + c^4 = \frac{b^4+b^4+b^4+c^4}{4} + \frac{b^4+c^4+c^4+c^4}{4} \geq \sqrt[4]{b^{12}c^4} + \sqrt[4]{b^4c^{12}} = b^3c + bc^3.$$
Tada za prvi izraz s lijeve strane početne nejednakosti vrijedi
$$\frac{a}{a+b^4+c^4} \leq \frac{a}{a+b^3c+bc^3} = \frac{a}{a+\frac{b^3c+bc^3}{abc}} = \frac{a}{a+\frac{b^2+c^2}{a}} = \frac{a^2}{a^2+b^2+c^2}.$$
Pritom smo u drugoj jednakosti iskoristili uvjet zadatka, budući da je dijeljenje nečega s $abc$ jednako kao da to dijelimo s $1$ - dakle ne mijenja vrijednost izraza. Primjenom istog postupka na preostala dva izraza iz početne nejednakost i zbrajanjem dobivenih nejednakosti, slijedi tvrdnja zadatka.
Ovo je teži zadatak. Ako ga niste sami uspjeli savladati, ne brinite. Važno je vidjeti i ovakve primjere i probati shvatiti motivaciju iza korištenih postupaka kako bi ih nakon nekog vremena i sami mogli primijenjivati. Uvjet zadatka i A-G su ovdje iskorišteni s motivacijom svođenja danih triju izraza na zajednički nazivnik - još jedan princip koji vrijedi imati na umu jer se nerijetko primjenjuje u zadacima s nejednakostima.
Ako ste spremni sami se okušati u zadacima s nejednakostima, upišite ,,DA'' kao rezultat!
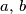 i
i  koji zadovoljavaju uvjet
koji zadovoljavaju uvjet 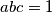 dokažite da vrijedi
dokažite da vrijedi 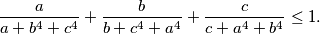
 , a ne
, a ne  . Možemo se zapitati, pa kako iskoristiti A-G nejednakost na način da neki članovi s desne strane zadane nejednakosti budu veći ili jednaki nekim članovima na lijevoj strani nejednakosti kada se desno nalazi samo jedinica?
. Možemo se zapitati, pa kako iskoristiti A-G nejednakost na način da neki članovi s desne strane zadane nejednakosti budu veći ili jednaki nekim članovima na lijevoj strani nejednakosti kada se desno nalazi samo jedinica?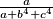 veći (ili jednak) od nekog
veći (ili jednak) od nekog  , onda će taj izraz zapravo biti manji (ili jednak) od
, onda će taj izraz zapravo biti manji (ili jednak) od 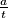 , što je smjer nejednakosti koji nam je potreban.
, što je smjer nejednakosti koji nam je potreban. je stupnja
je stupnja  dok je
dok je 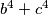 stupnja
stupnja  . Generalni princip je da je korisno imati homogen izraz jer nam to najčešće omogućuje smislenije primjene nejednakosti poput A-Ga i bolje faktorizacije. Način za postići homogenost je korištenje uvjeta zadatka. Imajmo to na umu jer ćemo u jednom trenutku rješenja htjeti provesti homogenizaciju u nazivniku.
. Generalni princip je da je korisno imati homogen izraz jer nam to najčešće omogućuje smislenije primjene nejednakosti poput A-Ga i bolje faktorizacije. Način za postići homogenost je korištenje uvjeta zadatka. Imajmo to na umu jer ćemo u jednom trenutku rješenja htjeti provesti homogenizaciju u nazivniku.![b^4 + c^4 = \frac{b^4+b^4+b^4+c^4}{4} + \frac{b^4+c^4+c^4+c^4}{4} \geq \sqrt[4]{b^{12}c^4} + \sqrt[4]{b^4c^{12}} = b^3c + bc^3.](/media/m/8/8/1/881faa89e5d405c14042bc3c8f55138e.png) Tada za prvi izraz s lijeve strane početne nejednakosti vrijedi
Tada za prvi izraz s lijeve strane početne nejednakosti vrijedi 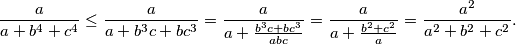 Pritom smo u drugoj jednakosti iskoristili uvjet zadatka, budući da je dijeljenje nečega s
Pritom smo u drugoj jednakosti iskoristili uvjet zadatka, budući da je dijeljenje nečega s 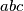 jednako kao da to dijelimo s
jednako kao da to dijelimo s  - dakle ne mijenja vrijednost izraza. Primjenom istog postupka na preostala dva izraza iz početne nejednakost i zbrajanjem dobivenih nejednakosti, slijedi tvrdnja zadatka.
- dakle ne mijenja vrijednost izraza. Primjenom istog postupka na preostala dva izraza iz početne nejednakost i zbrajanjem dobivenih nejednakosti, slijedi tvrdnja zadatka.