Metoda faktorizacije
Jedno od najzastupljenijih tema teorije brojeva na natjecanjima su diofantske jednadžbe. U širem smislu, to su jednadžbe u kojima nas zanimaju isključivo cjelobrojna rješenja. Zbog toga pri rješavanju ovih jednadžbi često promatramo pojmove poput djeljivosti i prostih brojeva.
Često korištena je metoda faktorizacije. Ideja je transformirati početne izraze u umnoške nekoliko manjih izraza. Tada se zadatak često svede na faktorizaciju nekog cijelog broja.
Primjer
Nađite sva cjelobrojna rješenja jednadžbe 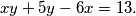
Rješenje
Izlučivanjem  na lijevoj strani dobivamo jednadžbu
na lijevoj strani dobivamo jednadžbu 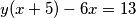 . Sada želimo i uz
. Sada želimo i uz  namjestiti faktor
namjestiti faktor 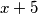 pa imamo
pa imamo 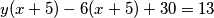 . Pritom smo morali dodati
. Pritom smo morali dodati  jer smo toliko oduzeli kako bi dobili faktor
jer smo toliko oduzeli kako bi dobili faktor 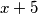 uz
uz  . Daljnjim izlučivanjem faktora
. Daljnjim izlučivanjem faktora 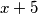 slijedi željeni oblik jednadžbe
slijedi željeni oblik jednadžbe 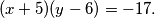 Kako je
Kako je  prost broj, imamo samo
prost broj, imamo samo  slučaja:
slučaja: 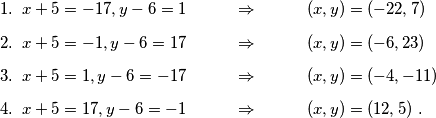
Kao rezultat upišite koliko rješenja (uređenih parova  ) ima diofantska jednadžba iz primjera ako na desnoj strani umjesto
) ima diofantska jednadžba iz primjera ako na desnoj strani umjesto  stoji
stoji 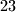 .
.
