Ideja ove metode je smanjiti skup mogućih rješenja korištenjem nejednakosti. Često to budu jednostavna opažanja, kao što vidimo u sljedećem primjeru.
Primjer
Nađite sve prirodne brojeve 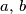 i
i  koji zadovoljavaju jednadžbu
koji zadovoljavaju jednadžbu 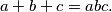
Rješenje
Bez smanjenja općenitosti (jer je jednadžba simetrična) možemo pretpostaviti da je 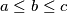 . Zato je
. Zato je 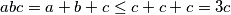 pa slijedi
pa slijedi 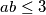 . Preostaju nam 3 slučaja:
. Preostaju nam 3 slučaja: 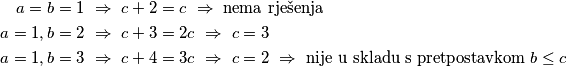 Dakle, sva rješenja su
Dakle, sva rješenja su 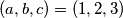 i sve simetrične kombinacije toga.
i sve simetrične kombinacije toga.
Kao rezultat upišite ukupan broj svih rješenja u primjeru.
Ideja ove metode je smanjiti skup mogućih rješenja korištenjem \textit{nejednakosti}. Često to budu jednostavna opažanja, kao što vidimo u sljedećem primjeru.
\textbf{Primjer}
Nađite sve prirodne brojeve $a, \, b$ i $c$ koji zadovoljavaju jednadžbu
$$a+b+c = abc.$$
\textbf{Rješenje}
Bez smanjenja općenitosti (jer je jednadžba simetrična) možemo pretpostaviti da je $a \leq b \leq c$. Zato je $abc = a+b+c \leq c + c + c = 3c$ pa slijedi $ab \leq 3$. Preostaju nam 3 slučaja:
\begin{align*}
a=b=1 \ &\Rightarrow \ c+2=c \ \Rightarrow \ \text{nema rješenja} \\
a=1, b=2 \ &\Rightarrow \ c+3=2c \ \Rightarrow \ c=3 \\
a=1, b=3 \ &\Rightarrow \ c+4=3c \ \Rightarrow \ c=2 \ \Rightarrow \ \text{nije u skladu s pretpostavkom } b \leq c \\
\end{align*}
Dakle, sva rješenja su $(a,b,c)=(1,2,3)$ i sve simetrične kombinacije toga.
Kao rezultat upišite ukupan broj svih rješenja u primjeru.
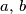 i
i  koji zadovoljavaju jednadžbu
koji zadovoljavaju jednadžbu 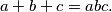
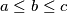 . Zato je
. Zato je 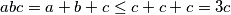 pa slijedi
pa slijedi 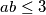 . Preostaju nam 3 slučaja:
. Preostaju nam 3 slučaja: 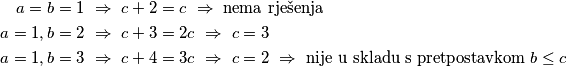 Dakle, sva rješenja su
Dakle, sva rješenja su 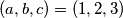 i sve simetrične kombinacije toga.
i sve simetrične kombinacije toga.