Još jedna standardna metoda pri rješavanju diofantskih jednadžbi je promatranje ostataka koje razni izrazi u jednadžbi daju pri dijeljenju s nekim brojem. Primjerice, pokažemo li da lijeva strana jednadžbe uvijek mora davati ostatke  ili
ili  pri dijeljenju s
pri dijeljenju s  , a da desna strana daje ostatak
, a da desna strana daje ostatak  , onda možemo zaključiti da jednadžba nema rješenja. Pritom često koristimo izraz oblika
, onda možemo zaključiti da jednadžba nema rješenja. Pritom često koristimo izraz oblika 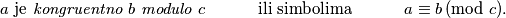 To znači da broj
To znači da broj  pri dijeljenju brojem
pri dijeljenju brojem  daje ostatak
daje ostatak  . Npr,
. Npr, 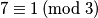 ili
ili 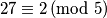 .
.
Primjer 1
Nađi sve prirodne brojeve brojeve  i
i  koji zadovoljavaju jednadžbu
koji zadovoljavaju jednadžbu 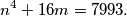
Rješenje
Kada bi  bio paran broj, lijeva strana jednadžbe bi bila parna, a desna je neparna pa u tom slučaju nema rješenja. Ako je
bio paran broj, lijeva strana jednadžbe bi bila parna, a desna je neparna pa u tom slučaju nema rješenja. Ako je  neparan, možemo ga zapisati kao
neparan, možemo ga zapisati kao 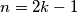 , za neki prirodan broj
, za neki prirodan broj  pa uvrštavanjem dobivamo
pa uvrštavanjem dobivamo 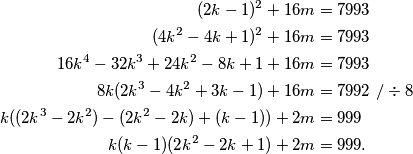 Kako su
Kako su  i
i  uzastopni prirodni brojevi, jedan od njih je paran pa su oba pribrojnika na lijevoj strani završne jednadžbe parna, dok je desna strana neparna. Zato ova jednadćba nema rješenja.
uzastopni prirodni brojevi, jedan od njih je paran pa su oba pribrojnika na lijevoj strani završne jednadžbe parna, dok je desna strana neparna. Zato ova jednadćba nema rješenja.
Primjer 2
Nađite sve prirodne brojeve  i
i  koji zadovoljavaju jednadžbu
koji zadovoljavaju jednadžbu 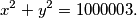
Rješenje Promotrimo ostatke koje kvadrat prirodnog broja može davati pri dijeljenju s  . To vidimo iz sljedeće tablice:
. To vidimo iz sljedeće tablice:
Dakle, suma dva potpuna kvadrata kao na lijevoj strani jednadžbe može poprimiti sve ostatke pri dijeljenju s  osim
osim  . No, broj na desnoj strani jednadžbe daje upravo ostatak
. No, broj na desnoj strani jednadžbe daje upravo ostatak  pri dijeljenju s
pri dijeljenju s  pa ni ova jednadžba nema rješenja.
pa ni ova jednadžba nema rješenja.
Sada ste spremni sami primijenjivati spomenute metode na zadacima! Upišite  kao rezultat.
kao rezultat.
Još jedna standardna metoda pri rješavanju diofantskih jednadžbi je promatranje ostataka koje razni izrazi u jednadžbi daju pri dijeljenju s nekim brojem. Primjerice, pokažemo li da lijeva strana jednadžbe uvijek mora davati ostatke $3$ ili $4$ pri dijeljenju s $5$, a da desna strana daje ostatak $0$, onda možemo zaključiti da jednadžba nema rješenja. Pritom često koristimo izraz oblika
$$a \text{ je} \textit{ kongruentno } b \textit{ modulo } c \hspace{1cm} \text{ ili simbolima } \hspace{1 cm} a \equiv b \, (\text{mod } c).$$
To znači da broj $a$ pri dijeljenju brojem $c$ daje ostatak $b$. Npr, $7 \equiv 1 \, (\text{mod } 3)$ ili $27 \equiv 2 \, (\text{mod } 5)$.
\textbf{Primjer 1}
Nađi sve prirodne brojeve brojeve $m$ i $n$ koji zadovoljavaju jednadžbu
$$n^4+16m=7993.$$
\textbf{Rješenje}
Kada bi $n$ bio paran broj, lijeva strana jednadžbe bi bila parna, a desna je neparna pa u tom slučaju nema rješenja.
Ako je $n$ neparan, možemo ga zapisati kao $n=2k-1$, za neki prirodan broj $k$ pa uvrštavanjem dobivamo
\begin{align*}
(2k-1)^2+16m &= 7993 \\
(4k^2-4k+1)^2+16m &= 7993 \\
16k^4-32k^3+24k^2-8k+1 + 16m &= 7993 \\
8k(2k^3-4k^2+3k-1) + 16m &= 7992\ /\div 8 \\
k((2k^3-2k^2)-(2k^2-2k)+(k-1)) + 2m &= 999 \\
k(k-1)(2k^2-2k+1) + 2m &= 999 \text.
\end{align*}
Kako su $k-1$ i $k$ uzastopni prirodni brojevi, jedan od njih je paran pa su oba pribrojnika na lijevoj strani završne jednadžbe parna, dok je desna strana neparna. Zato ova jednadćba nema rješenja.
\textbf{Primjer 2}
Nađite sve prirodne brojeve $x$ i $y$ koji zadovoljavaju jednadžbu
$$x^2+y^2=1000003.$$
\textbf{Rješenje}
Promotrimo ostatke koje kvadrat prirodnog broja može davati pri dijeljenju s $4$. To vidimo iz sljedeće tablice:
\begin{center}
\begin{tabular}{c | c | c | c | c}
$n$ & 0 & 1 & 2 & 3 \\
\hline
$n^2$ & 0 & 1 & 0 & 1
\end{tabular}
\end{center}
Dakle, suma dva potpuna kvadrata kao na lijevoj strani jednadžbe može poprimiti sve ostatke pri dijeljenju s $4$ osim $3$. No, broj na desnoj strani jednadžbe daje upravo ostatak $3$ pri dijeljenju s $4$ pa ni ova jednadžba nema rješenja.
Sada ste spremni sami primijenjivati spomenute metode na zadacima! Upišite $0$ kao rezultat.
 ili
ili  pri dijeljenju s
pri dijeljenju s  , a da desna strana daje ostatak
, a da desna strana daje ostatak  , onda možemo zaključiti da jednadžba nema rješenja. Pritom često koristimo izraz oblika
, onda možemo zaključiti da jednadžba nema rješenja. Pritom često koristimo izraz oblika 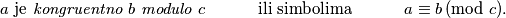 To znači da broj
To znači da broj  pri dijeljenju brojem
pri dijeljenju brojem  daje ostatak
daje ostatak  . Npr,
. Npr, 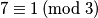 ili
ili 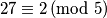 .
. i
i  koji zadovoljavaju jednadžbu
koji zadovoljavaju jednadžbu 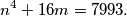
 bio paran broj, lijeva strana jednadžbe bi bila parna, a desna je neparna pa u tom slučaju nema rješenja. Ako je
bio paran broj, lijeva strana jednadžbe bi bila parna, a desna je neparna pa u tom slučaju nema rješenja. Ako je  neparan, možemo ga zapisati kao
neparan, možemo ga zapisati kao 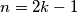 , za neki prirodan broj
, za neki prirodan broj  pa uvrštavanjem dobivamo
pa uvrštavanjem dobivamo 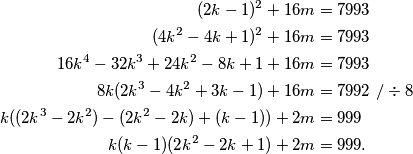 Kako su
Kako su  i
i  uzastopni prirodni brojevi, jedan od njih je paran pa su oba pribrojnika na lijevoj strani završne jednadžbe parna, dok je desna strana neparna. Zato ova jednadćba nema rješenja.
uzastopni prirodni brojevi, jedan od njih je paran pa su oba pribrojnika na lijevoj strani završne jednadžbe parna, dok je desna strana neparna. Zato ova jednadćba nema rješenja. i
i  koji zadovoljavaju jednadžbu
koji zadovoljavaju jednadžbu 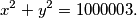
 . To vidimo iz sljedeće tablice:
. To vidimo iz sljedeće tablice: 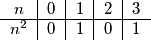
 osim
osim  . No, broj na desnoj strani jednadžbe daje upravo ostatak
. No, broj na desnoj strani jednadžbe daje upravo ostatak  pri dijeljenju s
pri dijeljenju s  pa ni ova jednadžba nema rješenja.
pa ni ova jednadžba nema rješenja. kao rezultat.
kao rezultat. 