Prvo rješenje
Primijenimo  nejednakost na prva dva člana s lijeve strane
nejednakost na prva dva člana s lijeve strane 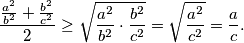 Analognom primjenom i na preostala
Analognom primjenom i na preostala  para članova na lijevoj strani početne nejednakosti i zbrajanjem tih triju izraza, dolazimo do tvrdnje koju je trebalo dokazati.
para članova na lijevoj strani početne nejednakosti i zbrajanjem tih triju izraza, dolazimo do tvrdnje koju je trebalo dokazati.
Drugo rješenje
Pomnožimo cijelu jednadžbu s 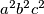 i prebacimo sve članove na istu stranu te ih pažljivo grupirajmo
i prebacimo sve članove na istu stranu te ih pažljivo grupirajmo 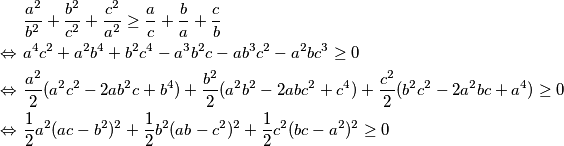 Posljednja nejednakost je očito istinita jer na lijevoj strani imamo sumu kvadrata realnih brojeva koji su nenegativni. Kako je posljednja nejednakost ispravna, mora vrijediti i početna te je tvrdnja dokazana.
Posljednja nejednakost je očito istinita jer na lijevoj strani imamo sumu kvadrata realnih brojeva koji su nenegativni. Kako je posljednja nejednakost ispravna, mora vrijediti i početna te je tvrdnja dokazana.
\textbf{Prvo rješenje}
Primijenimo $A-G$ nejednakost na prva dva člana s lijeve strane
$$\frac{\frac{a^2}{b^2} + \frac{b^2}{c^2}}{2} \geq \sqrt{\frac{a^2}{b^2} \cdot \frac{b^2}{c^2}} = \sqrt{\frac{a^2}{c^2}} = \frac{a}{c}.$$
Analognom primjenom i na preostala $2$ para članova na lijevoj strani početne nejednakosti i zbrajanjem tih triju izraza, dolazimo do tvrdnje koju je trebalo dokazati.
\textbf{Drugo rješenje}
Pomnožimo cijelu jednadžbu s $a^2b^2c^2$ i prebacimo sve članove na istu stranu te ih pažljivo grupirajmo
\begin{align*}
&\frac{a^2}{b^2} + \frac{b^2}{c^2} + \frac{c^2}{a^2} \geq \frac{a}{c} + \frac{b}{a} + \frac{c}{b} \\
\Leftrightarrow \ & a^4c^2 + a^2b^4 + b^2c^4 - a^3b^2c - ab^3c^2 - a^2bc^3 \geq 0 \\
\Leftrightarrow \ & \frac{a^2}{2}(a^2c^2 - 2ab^2c + b^4) + \frac{b^2}{2}(a^2b^2 - 2abc^2 + c^4) + \frac{c^2}{2}(b^2c^2 - 2a^2bc + a^4) \geq 0 \\
\Leftrightarrow \ & \frac{1}{2}a^2(ac-b^2)^2 + \frac{1}{2}b^2(ab-c^2)^2 + \frac{1}{2}c^2(bc-a^2)^2 \geq 0
\end{align*}
Posljednja nejednakost je očito istinita jer na lijevoj strani imamo sumu kvadrata realnih brojeva koji su nenegativni. Kako je posljednja nejednakost ispravna, mora vrijediti i početna te je tvrdnja dokazana.
 nejednakost na prva dva člana s lijeve strane
nejednakost na prva dva člana s lijeve strane 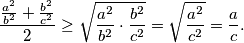 Analognom primjenom i na preostala
Analognom primjenom i na preostala  para članova na lijevoj strani početne nejednakosti i zbrajanjem tih triju izraza, dolazimo do tvrdnje koju je trebalo dokazati.
para članova na lijevoj strani početne nejednakosti i zbrajanjem tih triju izraza, dolazimo do tvrdnje koju je trebalo dokazati.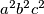 i prebacimo sve članove na istu stranu te ih pažljivo grupirajmo
i prebacimo sve članove na istu stranu te ih pažljivo grupirajmo 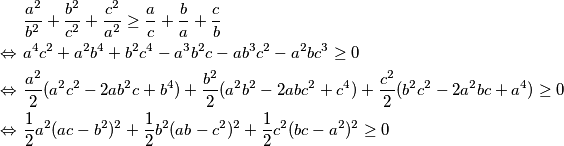 Posljednja nejednakost je očito istinita jer na lijevoj strani imamo sumu kvadrata realnih brojeva koji su nenegativni. Kako je posljednja nejednakost ispravna, mora vrijediti i početna te je tvrdnja dokazana.
Posljednja nejednakost je očito istinita jer na lijevoj strani imamo sumu kvadrata realnih brojeva koji su nenegativni. Kako je posljednja nejednakost ispravna, mora vrijediti i početna te je tvrdnja dokazana. 