Vrijeme: 01:56
Teorija brojeva: Diofantske jednadžbe 3 - RJEŠENJE
Prvo rješenje
U jednakosti 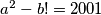 možemo promatrati ostatak pri dijeljenju sa
možemo promatrati ostatak pri dijeljenju sa  .
.
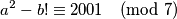
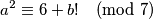
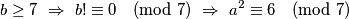 Kako kvadrat prirodnog broja ne može biti
Kako kvadrat prirodnog broja ne može biti 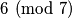 zaključujemo da je
zaključujemo da je 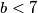 .
.
Uvrštavanjem 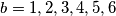 dobijamo da je jedino moguće rješenje
dobijamo da je jedino moguće rješenje 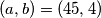 .
.
Drugo rješenje
Za 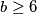 vrijedi da
vrijedi da  dijeli
dijeli 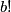 , jer
, jer 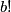 sadrži faktore
sadrži faktore  i
i  . Kako je
. Kako je 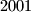 djeljiv s
djeljiv s  mora biti i
mora biti i  . Ako
. Ako  dijeli
dijeli  onda
onda  dijeli i
dijeli i  . Ali to znači da je lijeva strana djeljiva s
. Ali to znači da je lijeva strana djeljiva s  , a desna nije, što je kontradikcija. Preostaje nam još provjeriti za
, a desna nije, što je kontradikcija. Preostaje nam još provjeriti za 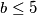 . Vidimo da je jedino rješenje
. Vidimo da je jedino rješenje 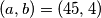 .
.
