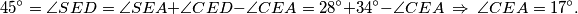MetaMath '22 - demo

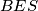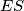Označimo s $S$ polovište dužine $\overline{AB}$, odnosno središte promatrane polukružnice. Primijetimo da je tada trokut $BES$ jednakokračan jer su $BS$ i $ES$ polumjeri pa je 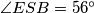$\angle ESB = 56^\circ$. Uz to, trokut 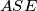$ASE$ je također jednakokračan i vrijedi 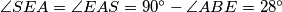$\angle SEA = \angle EAS = 90^\circ - \angle ABE = 28^\circ$. Nadalje, trokut 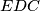$EDC$ je pravokutan pa je 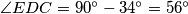$\angle EDC = 90^\circ - 34^\circ = 56^\circ$. Promotrimo li zbroj nasuprotnih kuteva u četverokutu 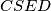$CSED$ dobivamo 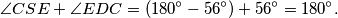$$\angle CSE + \angle EDC = (180^\circ - 56^\circ) + 56^\circ = 180^\circ.$$ Dakle, taj je četverokut tetivan pa su njegove stranice tetive njemu opisane kružnice i obodni kutevi nad njima moraju biti jednaki. 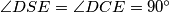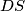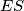Zato je $\angle DSE = \angle DCE = 90^\circ$, a k tome su $DS$ i $ES$ polumjeri promatrane polukružnice pa je trokut 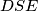$DSE$ jednakokračan i pravokutan. Sada imamo: $$45^\circ = \angle SED = \angle SEA + \angle CED - \angle CEA = 28^\circ + 34^\circ - \angle CEA \ \Rightarrow \ \angle CEA = 17^\circ.$$