MetaMath '22 - demo

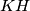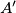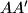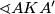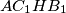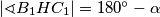Označimo sjecište pravca $KH$ i opisane kružnice s $A'$, a nožista visina iz vrhova $B$ i $C$ s $B_1$ i $C_1$. Primijetimo odmah da je $AA'$ promjer promatrane kružnice, budući da je $\sphericalangle AKA'$ pravi kut. Promotrimo četverokut $AC_1HB_1$ - kako su kutovi u vrhovima $B_1$ i $C_1$ pravi, zaključujemo da je $|\sphericalangle B_1HC_1| = 180^{\circ}-\alpha$. Nadalje, imamo 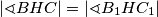$|\sphericalangle BHC| = |\sphericalangle B_1HC_1|$ jer su to vršni kutovi. Također, 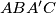$ABA'C$ je tetivan četverokut jer je 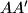$AA'$ promjer pa je 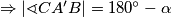$\Rightarrow |\sphericalangle CA'B| = 180^{\circ}-\alpha$. Sljedeće, vrijedi 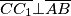$\overline{CC_1} \bot \overline{AB}$ jer je 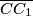$\overline{CC_1}$ visina trokuta te 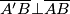$\overline{A'B} \bot \overline{AB}$ po Talesovom poučku o obodnom kutu nad promjerom kružnice.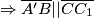 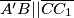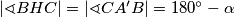$\ \Rightarrow \overline{A'B} || \overline{CC_1}$ Kako vrijedi $\overline{A'B} || \overline{CC_1}$ i $|\sphericalangle BHC| = |\sphericalangle CA'B| = 180^{\circ}-\alpha$, zaključujemo da je 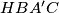$HBA'C$ paralelogram. Tada je sjecište 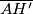$\overline{AH'}$ i $\overline{BC}$ polovište stranice $\overline{BC}$ jer se dijagonale paralelograma raspolavaljaju. Kako je 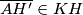$\overline{AH'} \in KH$ zaključujemo da pravac 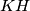$KH$ raspolavlja dužinu $\overline{BC}$.