Primijetimo da je $\sphericalangle FCA = \sphericalangle ABE$ jer je četverokut $AEBC$ tetivan. Dokažimo $\sphericalangle ABE = \sphericalangle AGH$ - dovoljno je pokazati da je četverokut $AHGB$ tetivan.
Četverokut $AFBD$ je tetivan pa je $\sphericalangle DAB = \sphericalangle DFB = x$. Ponovno koristimo činjenicu da je četverokut $AEBC$ tetivan odakle dobivamo $\sphericalangle CAB = \sphericalangle CEB = y$. Sada je iz $\sphericalangle CAB = \sphericalangle CAD + \sphericalangle DAB$ jasno da je $\sphericalangle CAD = y - x$.
Vrijedi $\sphericalangle HAG = \sphericalangle CAD = y - x$, jer su to vršni kutovi. Nadalje, vrijedi i $\sphericalangle CEB + \sphericalangle FEB = 180^\circ$, tj. kako je $\sphericalangle CEB = y$ imamo $\sphericalangle FEB = 180^\circ - y$. Iz trokuta $EFB$ proizlazi $\sphericalangle FEB + \sphericalangle DFB + \sphericalangle HBG = 180^\circ$ pa uvrštavajem poznatih kutova dobivamo $\sphericalangle HBG = y - x$.
Kako je $\sphericalangle HBG = \sphericalangle HAG = y - x$ slijedi da je četverokut $AHGB$ tetivan. Iz toga proizlazi da je $\sphericalangle AGH = \sphericalangle ABE$, što znači zbog $\sphericalangle ABE = \sphericalangle FCA$ da je $\sphericalangle FCA = \sphericalangle AGH$, a kako su to kutevi uz presječnicu $CG$, slijedi da su pravci $HG$ i $CF$ paralelni.
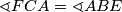 jer je četverokut
jer je četverokut 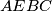 tetivan. Dokažimo
tetivan. Dokažimo 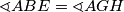 - dovoljno je pokazati da je četverokut
- dovoljno je pokazati da je četverokut 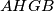 tetivan.
tetivan.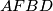 je tetivan pa je
je tetivan pa je 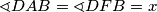 . Ponovno koristimo činjenicu da je četverokut
. Ponovno koristimo činjenicu da je četverokut 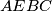 tetivan odakle dobivamo
tetivan odakle dobivamo 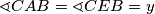 . Sada je iz
. Sada je iz 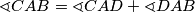 jasno da je
jasno da je 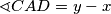 .
.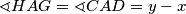 , jer su to vršni kutovi. Nadalje, vrijedi i
, jer su to vršni kutovi. Nadalje, vrijedi i 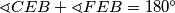 , tj. kako je
, tj. kako je 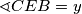 imamo
imamo 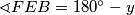 . Iz trokuta
. Iz trokuta 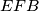 proizlazi
proizlazi 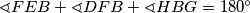 pa uvrštavajem poznatih kutova dobivamo
pa uvrštavajem poznatih kutova dobivamo 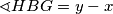 .
.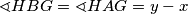 slijedi da je četverokut
slijedi da je četverokut 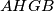 tetivan. Iz toga proizlazi da je
tetivan. Iz toga proizlazi da je 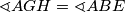 , što znači zbog
, što znači zbog 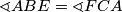 da je
da je 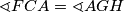 , a kako su to kutevi uz presječnicu
, a kako su to kutevi uz presječnicu 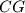 , slijedi da su pravci
, slijedi da su pravci 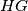 i
i 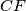 paralelni.
paralelni. 