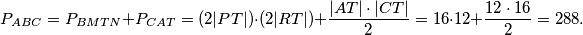Vrijeme: 01:56
Geometrija - Omjeri i površine: Težišnice - RJEŠENJE
Neka je težišnica iz vrha  do polovišta
do polovišta  stranice
stranice  duga
duga 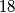 , a težišnica iz vrha
, a težišnica iz vrha  do polovišta
do polovišta  stranice
stranice  duga
duga 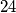 te neka se težišnice sijeku u težištu
te neka se težišnice sijeku u težištu  . Budući da težište dijeli težišnice u omjeru
. Budući da težište dijeli težišnice u omjeru 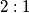 , zaključujemo da je
, zaključujemo da je 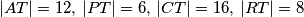 .
.
Produžimo težišnicu 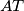 preko
preko  do točke
do točke  tako da je
tako da je 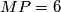 , a težišnicu
, a težišnicu 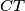 preko
preko  do točke
do točke  tako da je
tako da je 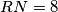 . Lako se vidi da su trokuti
. Lako se vidi da su trokuti 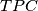 i
i 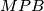 sukladni, kao i trokuti
sukladni, kao i trokuti 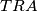 i
i 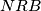 , po
, po 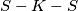 poučku. Iz toga onda slijedi da je
poučku. Iz toga onda slijedi da je 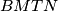 pravokutnik, jer su kutovi uz vrhove
pravokutnik, jer su kutovi uz vrhove  ,
,  i
i  pravi.
pravi.
Primijetimo da je 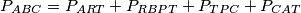 . No, zbog dokazanih sukladnosti vidimo da je
. No, zbog dokazanih sukladnosti vidimo da je 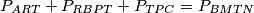 . Stoga je
. Stoga je