Vrijeme: 01:56
Geometrija - Omjeri i površine: Trapez - RJEŠENJE
Označimo vrhove trapeza redom  pri čemu je
pri čemu je  duža osnovica, a
duža osnovica, a  kraća. Uvedimo oznake
kraća. Uvedimo oznake 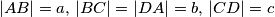 . Neka su
. Neka su  i
i  redom nožišta visina iz vrhova
redom nožišta visina iz vrhova  i
i  na osnovicu
na osnovicu  . Jasno je da su trokuti
. Jasno je da su trokuti 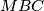 i
i 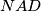 sukladni, a očito je i
sukladni, a očito je i 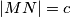 . Zato je
. Zato je 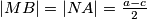 .
.
Promotrimo trokut 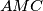 . On je pravokutan i vrijedi
. On je pravokutan i vrijedi 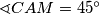 pa je zato i jednakokračan. Zato je
pa je zato i jednakokračan. Zato je 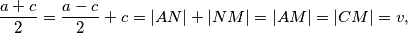 pri čemu je
pri čemu je  duljina visina na dužu osnovicu. Kako je hipotenuza u promatranom trokutu duljine
duljina visina na dužu osnovicu. Kako je hipotenuza u promatranom trokutu duljine  , vrijedi
, vrijedi 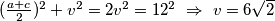 .
.
Za kraj, po formuli za površinu trapeza dobivamo: