Vrijeme: 20:51

Bojanja: Minus i plus - RJEŠENJE

Obojajmo sva polja u srednjem (trećem) retku ploče crnom bojom, a sva ostala obojajmo bijelom. Primijetimo da će odabir bilo kojeg kvadrata 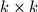k \times k, k>1 rezultirati odabirom parnog broja bijelih polja. Stoga, prilikom izvođenja bilo kojeg poteza neće se promijeniti parnost broja polja označenih s -1 među bijelim poljima. Dakle, ako se na početku -1 nalazi na nekom od bijelih polja, nećemo moći postići konfiguraciju u kojoj na ploči nema niti jednog polja označenog s -1 jer će među bijelim poljima uvijek biti neparan broj oznaka -1, dakle barem jedna u svakom trenutku.

Analogno možemo obojati sva polja u srednjem (trećem) stupcu ploče crnom bojom, a sva ostala bijelom i primijeniti jednaku argumentaciju. Prema dosadašnjim razmatranjima, znamo da se -1 na početku ne može nalaziti ni na kojem polju osim eventualno na središnjem.

Doista, u tom slučaju postoji niz poteza kojim postižemo uklanjanje svih oznaka -1 s ploče. Lako se provjeri da je jedan od takvih nizova upravo sljedeći: \begin{enumerate} \item Biramo $3 \times 3$ kvadrat kojem je gornje lijevo polje $(1,3)$. \item Biramo $3 \times 3$ kvadrat kojem je gornje lijevo polje $(3,1)$. \item Biramo $2 \times 2$ kvadrat kojem je gornje lijevo polje $(4,4)$. \item Biramo $2 \times 2$ kvadrat kojem je gornje lijevo polje $(1,1)$. \item Biramo $5 \times 5$ kvadrat kojem je gornje lijevo polje $(1,1)$. \end{enumerate}