Ukoliko se u nekom trenutku na istom polju nalazi više buba, primijetimo da ih možemo tretirati kao jednu bubu. Dokazati ćemo da je moguće dovesti sve bube na ploču 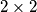 u lijevom gornjem kutu ploče. Primijetimo da za svaki
u lijevom gornjem kutu ploče. Primijetimo da za svaki 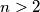 , sve bube iz polja
, sve bube iz polja 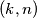 ,
,  , mogu preći u polje
, mogu preći u polje 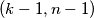 , dok buba iz polja
, dok buba iz polja 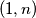 može preći u polje
može preći u polje 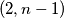 . Analogno, bube iz polja
. Analogno, bube iz polja 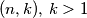 , mogu preći u polje
, mogu preći u polje 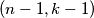 , dok buba iz polja
, dok buba iz polja 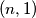 može preći u polje
može preći u polje 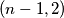 . Dakle, u jednom potezu možemo sve bube iz gornjeg lijevog kvadrata
. Dakle, u jednom potezu možemo sve bube iz gornjeg lijevog kvadrata  dovesti u gornji lijevi kvadrat
dovesti u gornji lijevi kvadrat 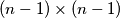 . Dakle, konačnim nizom poteza možemo dovesti bube iz početnog kvadrata
. Dakle, konačnim nizom poteza možemo dovesti bube iz početnog kvadrata 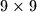 u gornji lijevi kvadrat
u gornji lijevi kvadrat 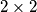 .
.
Time smo pokazali da bube možemo svesti na  polja. Dokažimo da ne možemo manje od toga. Promatranjem parnosti koordinata polja na kojem se buba nalazi zaključujemo da se prilikom poteza događaju prijelazi:
polja. Dokažimo da ne možemo manje od toga. Promatranjem parnosti koordinata polja na kojem se buba nalazi zaključujemo da se prilikom poteza događaju prijelazi: 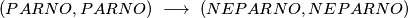
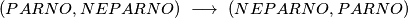
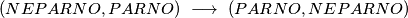
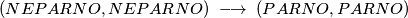 Kako na početku postoji barem
Kako na početku postoji barem  buba na svakom od
buba na svakom od  tipa polja po parnosti koordinata, primjećujemo da će i nakon svakog poteza uvijek postojati barem
tipa polja po parnosti koordinata, primjećujemo da će i nakon svakog poteza uvijek postojati barem  buba na svakom od tih tipova polja. Iz tog je razloga najmanji mogući broj upravo
buba na svakom od tih tipova polja. Iz tog je razloga najmanji mogući broj upravo  .
.
Ukoliko se u nekom trenutku na istom polju nalazi više buba, primijetimo da ih možemo tretirati kao jednu bubu. Dokazati ćemo da je moguće dovesti sve bube na ploču $2 \times 2$ u lijevom gornjem kutu ploče. Primijetimo da za svaki $n>2$, sve bube iz polja $(k,n)$, $k>1$, mogu preći u polje $(k-1,n-1)$, dok buba iz polja $(1,n)$ može preći u polje $(2,n-1)$. Analogno, bube iz polja $(n,k), \, k>1$, mogu preći u polje $(n-1,k-1)$, dok buba iz polja $(n,1)$ može preći u polje $(n-1,2)$. Dakle, u jednom potezu možemo sve bube iz gornjeg lijevog kvadrata $n \times n$ dovesti u gornji lijevi kvadrat $(n-1) \times (n-1)$. Dakle, konačnim nizom poteza možemo dovesti bube iz početnog kvadrata $9 \times 9$ u gornji lijevi kvadrat $2 \times 2$.
Time smo pokazali da bube možemo svesti na $4$ polja. Dokažimo da ne možemo manje od toga. Promatranjem parnosti koordinata polja na kojem se buba nalazi zaključujemo da se prilikom poteza događaju prijelazi:
$$(PARNO, PARNO) \ \longrightarrow \ (NEPARNO, NEPARNO)$$
$$(PARNO, NEPARNO) \ \longrightarrow \ (NEPARNO, PARNO)$$
$$(NEPARNO, PARNO) \ \longrightarrow \ (PARNO, NEPARNO)$$
$$(NEPARNO, NEPARNO) \ \longrightarrow \ (PARNO, PARNO)$$
Kako na početku postoji barem $1$ buba na svakom od $4$ tipa polja po parnosti koordinata, primjećujemo da će i nakon svakog poteza uvijek postojati barem $1$ buba na svakom od tih tipova polja. Iz tog je razloga najmanji mogući broj upravo $4$.
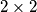 u lijevom gornjem kutu ploče. Primijetimo da za svaki
u lijevom gornjem kutu ploče. Primijetimo da za svaki 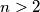 , sve bube iz polja
, sve bube iz polja 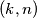 ,
,  , mogu preći u polje
, mogu preći u polje 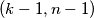 , dok buba iz polja
, dok buba iz polja 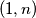 može preći u polje
može preći u polje 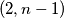 . Analogno, bube iz polja
. Analogno, bube iz polja 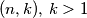 , mogu preći u polje
, mogu preći u polje 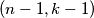 , dok buba iz polja
, dok buba iz polja 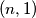 može preći u polje
može preći u polje 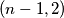 . Dakle, u jednom potezu možemo sve bube iz gornjeg lijevog kvadrata
. Dakle, u jednom potezu možemo sve bube iz gornjeg lijevog kvadrata  dovesti u gornji lijevi kvadrat
dovesti u gornji lijevi kvadrat 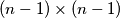 . Dakle, konačnim nizom poteza možemo dovesti bube iz početnog kvadrata
. Dakle, konačnim nizom poteza možemo dovesti bube iz početnog kvadrata 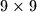 u gornji lijevi kvadrat
u gornji lijevi kvadrat 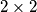 .
. polja. Dokažimo da ne možemo manje od toga. Promatranjem parnosti koordinata polja na kojem se buba nalazi zaključujemo da se prilikom poteza događaju prijelazi:
polja. Dokažimo da ne možemo manje od toga. Promatranjem parnosti koordinata polja na kojem se buba nalazi zaključujemo da se prilikom poteza događaju prijelazi: 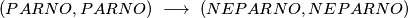
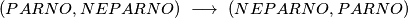
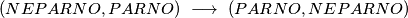
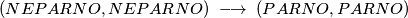 Kako na početku postoji barem
Kako na početku postoji barem  buba na svakom od
buba na svakom od  tipa polja po parnosti koordinata, primjećujemo da će i nakon svakog poteza uvijek postojati barem
tipa polja po parnosti koordinata, primjećujemo da će i nakon svakog poteza uvijek postojati barem  buba na svakom od tih tipova polja. Iz tog je razloga najmanji mogući broj upravo
buba na svakom od tih tipova polja. Iz tog je razloga najmanji mogući broj upravo  .
. 