Kombinatorna geometrija: Trokuti - RJEŠENJE
Budući da je točaka konačno, one čine konačan broj trokuta, pa među tim trokutima postoji trokut maksimalne površine (trokut  ). Promotrimo trokut kojem su
). Promotrimo trokut kojem su 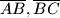 i
i  srednjice i nazovimo ga
srednjice i nazovimo ga 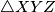 . Površina tog trokuta točno je
. Površina tog trokuta točno je  puta veća od površine trokuta
puta veća od površine trokuta  , dakle nije veća od
, dakle nije veća od  , a mi tvrdimo da su sve točke iz skupa unutar tog trokuta. Pretpostavimo suprotno, da se točka
, a mi tvrdimo da su sve točke iz skupa unutar tog trokuta. Pretpostavimo suprotno, da se točka  nalazi izvan trokuta. Tada se ona nalazi s druge strane barem jednog od pravaca
nalazi izvan trokuta. Tada se ona nalazi s druge strane barem jednog od pravaca  ,
, 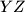 i
i 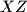 . Bez smanjenja općenitosti možemo pretpostaviti da se nalazi s druge strane pravca
. Bez smanjenja općenitosti možemo pretpostaviti da se nalazi s druge strane pravca  , koji je paralelan s
, koji je paralelan s  . Tada je površina trokuta
. Tada je površina trokuta 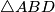 veća od površine trokuta
veća od površine trokuta  (imaju zajedničku stranicu
(imaju zajedničku stranicu  , a
, a 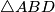 ima dulju visinu. To je u suprotnosti s pretpostavkom da
ima dulju visinu. To je u suprotnosti s pretpostavkom da  ima najveću površinu. Dakle, takva točka
ima najveću površinu. Dakle, takva točka  ne postoji i sve se nalaze unutar trokuta
ne postoji i sve se nalaze unutar trokuta 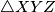 .
.
