Promatrajmo najveći zajedničkii djelitelj brojeva  i
i  u paru koordinata
u paru koordinata 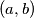 . Potezom prvog tipa udvostručujemo neku od koordinata što može dovesti do udvostručenja najvećeg zajedničkog djelitelja, ili ga ostavlja jednakim. Potezom drugog tipa oduzimamo manji član od većega čime se također ne mijenja najveći zajednički djelitelj. Dakle, ako su
. Potezom prvog tipa udvostručujemo neku od koordinata što može dovesti do udvostručenja najvećeg zajedničkog djelitelja, ili ga ostavlja jednakim. Potezom drugog tipa oduzimamo manji član od većega čime se također ne mijenja najveći zajednički djelitelj. Dakle, ako su 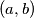 brojevi prije poteza, a
brojevi prije poteza, a 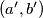 nakon poteza, vrijedi
nakon poteza, vrijedi 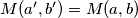 ili
ili 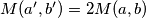 . Kako je početni najveći zajednički djelitelj
. Kako je početni najveći zajednički djelitelj  , vidimo da će u svakom trenutku najveći zajednički djelitelj biti neka potencija broja
, vidimo da će u svakom trenutku najveći zajednički djelitelj biti neka potencija broja  . Zato su jedine potencijalno dostižne točke nužno oblika
. Zato su jedine potencijalno dostižne točke nužno oblika 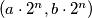 , pri čemu je
, pri čemu je 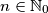 i
i 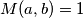 .
.
Pokažimo da je zaista svaka takva točka dostižna. Kako je 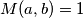 , barem jedan od tih brojeva je neparan. Bez smanjenja općenitosti, neka je to
, barem jedan od tih brojeva je neparan. Bez smanjenja općenitosti, neka je to  . Udvostručimo prvu koordinatu
. Udvostručimo prvu koordinatu  puta tako da je
puta tako da je 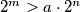 , a drugu koordinatu točno
, a drugu koordinatu točno  puta. Došli smo do točke
puta. Došli smo do točke 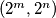 . Sada oduzmimo
. Sada oduzmimo 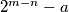 puta drugu koordinatu od prve. Time dolazimo do točke
puta drugu koordinatu od prve. Time dolazimo do točke 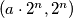 . Neka je sada
. Neka je sada  takav da je
takav da je 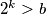 . Budući da je
. Budući da je  neparan, brojevi
neparan, brojevi 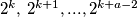 čine reducirani sustav ostataka pri dijeljenju s
čine reducirani sustav ostataka pri dijeljenju s  , odnosno među tih
, odnosno među tih  brojeva su svi mogući ostatci pri dijeljenju s
brojeva su svi mogući ostatci pri dijeljenju s  osim
osim  . Tada postoji
. Tada postoji  takav da je
takav da je 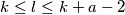 i
i 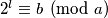 . Drugim riječima, postoji prirodan broj
. Drugim riječima, postoji prirodan broj  takav da je
takav da je 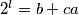 . Udvostručimo sada drugu koordinatu
. Udvostručimo sada drugu koordinatu  puta - time dolazimo do točke
puta - time dolazimo do točke 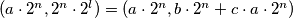 . Preostaje
. Preostaje  puta oduzeti prvu koordinatu od druge i dolazimo do željene točke.go
puta oduzeti prvu koordinatu od druge i dolazimo do željene točke.go
-------------------------------
NAPOMENA: Drugi dio rješenja nije ispravan, jer brojevi 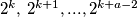 ne moraju činiti reducirani sustav ostataka pri dijeljenju s
ne moraju činiti reducirani sustav ostataka pri dijeljenju s  (recimo za
(recimo za 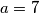 ). Zaključak stoga nije ispravan, recimo kontraprimjer je
). Zaključak stoga nije ispravan, recimo kontraprimjer je 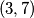 koji ne može biti postignut.
koji ne može biti postignut.
Promatrajmo najveći zajedničkii djelitelj brojeva $a$ i $b$ u paru koordinata $(a,b)$. Potezom prvog tipa udvostručujemo neku od koordinata što može dovesti do udvostručenja najvećeg zajedničkog djelitelja, ili ga ostavlja jednakim. Potezom drugog tipa oduzimamo manji član od većega čime se također ne mijenja najveći zajednički djelitelj. Dakle, ako su $(a,b)$ brojevi prije poteza, a $(a',b')$ nakon poteza, vrijedi $M(a',b')=M(a,b)$ ili $M(a',b')=2M(a,b)$. Kako je početni najveći zajednički djelitelj $1$, vidimo da će u svakom trenutku najveći zajednički djelitelj biti neka potencija broja $2$. Zato su jedine potencijalno dostižne točke nužno oblika $(a \cdot 2^n, b \cdot 2^n)$, pri čemu je $n \in \mathbb{N}_0$ i $M(a,b)=1$.
Pokažimo da je zaista svaka takva točka dostižna. Kako je $M(a,b)=1$, barem jedan od tih brojeva je neparan. Bez smanjenja općenitosti, neka je to $a$. Udvostručimo prvu koordinatu $m$ puta tako da je $2^m > a \cdot 2^n$, a drugu koordinatu točno $n$ puta. Došli smo do točke $(2^m, 2^n)$. Sada oduzmimo $2^{m-n} - a$ puta drugu koordinatu od prve. Time dolazimo do točke $(a \cdot 2^n, 2^n)$. Neka je sada $k \in \mathbb{N}$ takav da je $2^k>b$. Budući da je $a$ neparan, brojevi $2^k, \, 2^{k+1}, ..., 2^{k+a-2}$ čine reducirani sustav ostataka pri dijeljenju s $a$, odnosno među tih $a-1$ brojeva su svi mogući ostatci pri dijeljenju s $a$ osim $0$. Tada postoji $l$ takav da je $k \leq l \leq k+a-2$ i $2^l \equiv b \pmod{a}$. Drugim riječima, postoji prirodan broj $c$ takav da je $2^l = b + ca$. Udvostručimo sada drugu koordinatu $l$ puta - time dolazimo do točke $(a \cdot 2^n, 2^n \cdot 2^l) = (a \cdot 2^n, b \cdot 2^n + c \cdot a \cdot 2^n)$. Preostaje $c$ puta oduzeti prvu koordinatu od druge i dolazimo do željene točke.go
-------------------------------
NAPOMENA: Drugi dio rješenja nije ispravan, jer brojevi $2^k, \, 2^{k+1}, ..., 2^{k+a-2}$ ne moraju činiti reducirani sustav ostataka pri dijeljenju s $a$ (recimo za $a=7$). Zaključak stoga nije ispravan, recimo kontraprimjer je $(3,7)$ koji ne može biti postignut.
 i
i  u paru koordinata
u paru koordinata 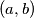 . Potezom prvog tipa udvostručujemo neku od koordinata što može dovesti do udvostručenja najvećeg zajedničkog djelitelja, ili ga ostavlja jednakim. Potezom drugog tipa oduzimamo manji član od većega čime se također ne mijenja najveći zajednički djelitelj. Dakle, ako su
. Potezom prvog tipa udvostručujemo neku od koordinata što može dovesti do udvostručenja najvećeg zajedničkog djelitelja, ili ga ostavlja jednakim. Potezom drugog tipa oduzimamo manji član od većega čime se također ne mijenja najveći zajednički djelitelj. Dakle, ako su 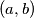 brojevi prije poteza, a
brojevi prije poteza, a 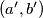 nakon poteza, vrijedi
nakon poteza, vrijedi 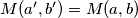 ili
ili 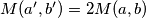 . Kako je početni najveći zajednički djelitelj
. Kako je početni najveći zajednički djelitelj  , vidimo da će u svakom trenutku najveći zajednički djelitelj biti neka potencija broja
, vidimo da će u svakom trenutku najveći zajednički djelitelj biti neka potencija broja  . Zato su jedine potencijalno dostižne točke nužno oblika
. Zato su jedine potencijalno dostižne točke nužno oblika 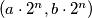 , pri čemu je
, pri čemu je 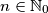 i
i 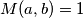 .
.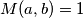 , barem jedan od tih brojeva je neparan. Bez smanjenja općenitosti, neka je to
, barem jedan od tih brojeva je neparan. Bez smanjenja općenitosti, neka je to  . Udvostručimo prvu koordinatu
. Udvostručimo prvu koordinatu  puta tako da je
puta tako da je 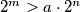 , a drugu koordinatu točno
, a drugu koordinatu točno  puta. Došli smo do točke
puta. Došli smo do točke 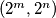 . Sada oduzmimo
. Sada oduzmimo 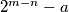 puta drugu koordinatu od prve. Time dolazimo do točke
puta drugu koordinatu od prve. Time dolazimo do točke 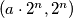 . Neka je sada
. Neka je sada  takav da je
takav da je 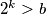 . Budući da je
. Budući da je  neparan, brojevi
neparan, brojevi 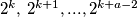 čine reducirani sustav ostataka pri dijeljenju s
čine reducirani sustav ostataka pri dijeljenju s  , odnosno među tih
, odnosno među tih  brojeva su svi mogući ostatci pri dijeljenju s
brojeva su svi mogući ostatci pri dijeljenju s  osim
osim  . Tada postoji
. Tada postoji  takav da je
takav da je 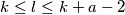 i
i 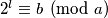 . Drugim riječima, postoji prirodan broj
. Drugim riječima, postoji prirodan broj  takav da je
takav da je 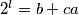 . Udvostručimo sada drugu koordinatu
. Udvostručimo sada drugu koordinatu  puta - time dolazimo do točke
puta - time dolazimo do točke 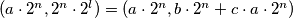 . Preostaje
. Preostaje  puta oduzeti prvu koordinatu od druge i dolazimo do željene točke.go
puta oduzeti prvu koordinatu od druge i dolazimo do željene točke.go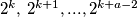 ne moraju činiti reducirani sustav ostataka pri dijeljenju s
ne moraju činiti reducirani sustav ostataka pri dijeljenju s  (recimo za
(recimo za 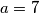 ). Zaključak stoga nije ispravan, recimo kontraprimjer je
). Zaključak stoga nije ispravan, recimo kontraprimjer je 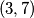 koji ne može biti postignut.
koji ne može biti postignut. 