Invarijante: Neprijateljski ambasadori - RJEŠENJE
Posjednimo na početku ambasadore na proizvoljan način. Neka je  broj susjednih parova neprijateljskih ambasadora. Pokažimo da u slučaju
broj susjednih parova neprijateljskih ambasadora. Pokažimo da u slučaju 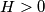 možemo napraviti razmještaj nekih ambasadora kojim smanjujemo
možemo napraviti razmještaj nekih ambasadora kojim smanjujemo  .
.
Neka su  i
i  susjedni neprijateljski ambasadori pri čemu
susjedni neprijateljski ambasadori pri čemu  sjedi desno od
sjedi desno od  . Ambasador
. Ambasador  ima barem
ima barem  prijatelja među preostalih
prijatelja među preostalih 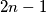 ambasadora. Odaberimo nekih
ambasadora. Odaberimo nekih  među njima i promotrimo mjesta koja se nalaze njima zdesna. Na tih
među njima i promotrimo mjesta koja se nalaze njima zdesna. Na tih  mjesta mora postojati barem
mjesta mora postojati barem  prijatelj ambasadora
prijatelj ambasadora  budući da on ima maksimalno
budući da on ima maksimalno  neprijatelja. Nazovimo tog ambasadora
neprijatelja. Nazovimo tog ambasadora 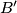 , a njegovog lijevog susjeda
, a njegovog lijevog susjeda 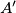 - on je ujedno i prijatelja ambasadora
- on je ujedno i prijatelja ambasadora  . Promotrimo sada luk od ambasadora
. Promotrimo sada luk od ambasadora  u smjeru suprotnom od kazaljke na satu, sve do ambasadora
u smjeru suprotnom od kazaljke na satu, sve do ambasadora 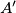 . Neka se on sastoji od ambasadora
. Neka se on sastoji od ambasadora 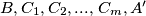 . Napravimo sada inverziju tog luka, odnosno zamijenimo mjesta ambasadorima
. Napravimo sada inverziju tog luka, odnosno zamijenimo mjesta ambasadorima  i
i 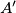 te ambasadorima
te ambasadorima 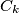 i
i 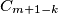 , za svaki
, za svaki 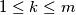 (ako je
(ako je  neparan onda ambasador
neparan onda ambasador 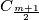 ostaje na svom mjestu). Primjetimo da su ovom transofrmacijom jedini ambasadori kojima se promijenio jedan od susjeda upravo ambasadori
ostaje na svom mjestu). Primjetimo da su ovom transofrmacijom jedini ambasadori kojima se promijenio jedan od susjeda upravo ambasadori 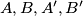 . Zbog odabira ambasadora
. Zbog odabira ambasadora 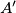 i
i 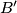 , znamo da su
, znamo da su  i
i 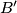 prijatelji, kao i
prijatelji, kao i  i
i 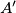 , pa se
, pa se  sigurno smanjio barem za
sigurno smanjio barem za  jer su
jer su  i
i  bili neprijateljski susjedi (a možda su takvi bili i
bili neprijateljski susjedi (a možda su takvi bili i 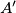 i
i 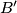 pa se
pa se  smanjio za
smanjio za  ). U svakom slučaju, našli smo transformaciju kojom se
). U svakom slučaju, našli smo transformaciju kojom se  strogo smanjuje za barem
strogo smanjuje za barem  , a on je na početku konačan pa će konačnim nizom ovakvih poteza postati
, a on je na početku konačan pa će konačnim nizom ovakvih poteza postati  :
:
