Vrijeme: 01:56
Kombinatorna geometrija: Kopunktualni pravci - RJEŠENJE
Promotrimo skup 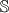 svih sjecišta promatranih pravaca. Neka je
svih sjecišta promatranih pravaca. Neka je 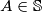 i
i  pravac takvi da je udaljenost među njima minimalna među svim mogućima udaljenostima neke točke iz
pravac takvi da je udaljenost među njima minimalna među svim mogućima udaljenostima neke točke iz 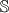 od nekog od promatranih pravaca. Kroz točku
od nekog od promatranih pravaca. Kroz točku  prolaze barem
prolaze barem  pravca, a kako nijedan nije paralelan s
pravca, a kako nijedan nije paralelan s  , pretpostavimo da ga sijeku redom u točkama
, pretpostavimo da ga sijeku redom u točkama 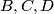 . Neka je
. Neka je  nožište okomice iz
nožište okomice iz  na
na  . Neke
. Neke  točke među
točke među 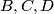 moraju se nalaziti s iste strane točke
moraju se nalaziti s iste strane točke  na pravcu
na pravcu  - pretpostavimo da su to
- pretpostavimo da su to  i
i  te neka je
te neka je 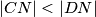 . Sada imamo pravokutan trokut
. Sada imamo pravokutan trokut 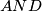 i točku
i točku  na jednoj od njegovih kateta te je jasno da je okomica iz nje na hipotenuzu
na jednoj od njegovih kateta te je jasno da je okomica iz nje na hipotenuzu 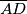 kraća od
kraća od 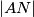 , što je kontradikcija s pretpostavkom da smo odabrali par
, što je kontradikcija s pretpostavkom da smo odabrali par  i
i  za koji je udaljenost najmanja.
za koji je udaljenost najmanja.
