Vrijeme: 01:56
Kombinatorna geometrija: Loptanje - RJEŠENJE
U zadatku smo zaboravili navesti pretpostavku da ne postoje  para djevojčica koje su jednako udaljene. Ovdje je rješenje uz tu pretpostavku.
para djevojčica koje su jednako udaljene. Ovdje je rješenje uz tu pretpostavku.
Pretpostavimo suprotno, odnosno da postoji djevojčica  koja će dobiti barem
koja će dobiti barem  lopti i neka je to redom (u smjeru kazaljke na satu) od djevojčica
lopti i neka je to redom (u smjeru kazaljke na satu) od djevojčica 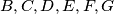 . Primijetimo da je
. Primijetimo da je 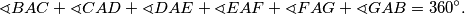 Zato je jedan od
Zato je jedan od  kuteva u sumi manji ili jednak
kuteva u sumi manji ili jednak 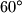 - bez smanjenja općenitosti neka je to
- bez smanjenja općenitosti neka je to 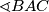 . Kako znamo da trokut
. Kako znamo da trokut  nije jednakostraničan, vrijedi
nije jednakostraničan, vrijedi 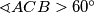 ili
ili 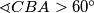 . No, onda je dužina
. No, onda je dužina  kraća od dužine
kraća od dužine  ili od dužine
ili od dužine  što znači da jedna od djevojčica
što znači da jedna od djevojčica  i
i  neće baciti loptu djevojčici
neće baciti loptu djevojčici  nego drugoj djevojčici iz promatranog trokuta, a to je kontradikcija s pretpostavkom.
nego drugoj djevojčici iz promatranog trokuta, a to je kontradikcija s pretpostavkom.
