Vrijeme: 18:51
Juniori #3
Konveksni četverokut 
dijeli kružnicu na osam kružnih lukova tako da četiri luka leže unutar četverokuta, a ostala četiri izvan. Označimo duljine lukova koji leže unutar četverokuta redom s 
, 
, 
i 
(u smjeru suprotnom od kazaljke na satu, počevši od proizvoljnog luka).
Dokaži da je četverokut tetivan ako i samo ako vrijedi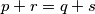 
.