Točno
16. travnja 2012. 07:49 (13 godine, 10 mjeseci)
Neka je

te
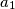
,
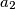
, ...,
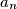
pozitivni realni brojevi za koje vrijedi
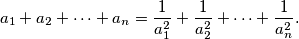
Dokaži da za svaki
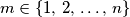
postoji

brojeva iz skupa
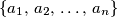
čiji je zbroj barem

.
%V0
Neka je $n \in \mathbb{N}$ te $a_{1}$, $a_{2}$, ..., $a_{n}$ pozitivni realni brojevi za koje vrijedi $$ a_{1} + a_{2} + \cdots + a_{n} = \frac{1}{a_{1}^{2}} + \frac{1}{a_{2}^{2}} + \cdots + \frac{1}{a_{n}^{2}} \text{.} $$
Dokaži da za svaki $m \in \left\{1,\,2,\,\ldots,\,n\right\}$ postoji $m$ brojeva iz skupa $\left\{a_{1},\,a_{2},\,\ldots,\,a_{n}\right\}$ čiji je zbroj barem $m$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Prvo ćemo dokazati da je
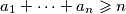
, a zatim ostatak zadatka dokazati indukcijom.
Pretpostavimo da je
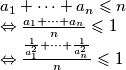
Iz A-G nejednakosti i prvog izraza dobivamo dobivamo
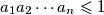
a iz drugog izraza
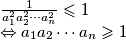
što je kontradikcija.
Dakle mora vrjediti
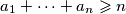
Označimo najmanji broj skupa s

Pretpostavimo da je
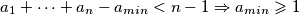
, ali i
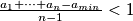
, kako aritmetička sredina nikad nije manja od svih svojih članova, znamo da postoji

takav da
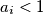
ali istovremeno i
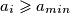
što je kontradikcija s
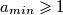
.
Dakle tvrdnja vrijedi za svaki
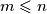
.
%V0
Prvo ćemo dokazati da je $a_1+ \cdots + a_n \geqslant n$, a zatim ostatak zadatka dokazati indukcijom.
Pretpostavimo da je
$a_1 + \cdots + a_n \leqslant n \newline \Leftrightarrow \frac{a_1+ \cdots + a_n}{n} \leqslant 1\newline \Leftrightarrow \frac{\frac{1}{a_1^2}+ \cdots + \frac{1}{a_n^2}}{n} \leqslant 1$
Iz A-G nejednakosti i prvog izraza dobivamo dobivamo
$a_1a_2 \cdots a_n \leqslant 1$
a iz drugog izraza
$ \frac{1}{a_1^2a_2^2 \cdots a_n^2} \leqslant 1\newline\Leftrightarrow a_1a_2 \cdots a_n \geqslant 1 $
što je kontradikcija.
Dakle mora vrjediti $a_1 + \cdots + a_n \geqslant n$
Označimo najmanji broj skupa s $a_{min}$
Pretpostavimo da je $a_1 + \cdots + a_n - a_{min} < n-1\Rightarrow a_{min} \geqslant 1$, ali i
$\frac{a_1 + \cdots + a_n - a_{min}}{n-1} < 1$, kako aritmetička sredina nikad nije manja od svih svojih članova, znamo da postoji $i$ takav da $a_i < 1$ ali istovremeno i $a_i \geqslant a_{min}$ što je kontradikcija s $a_{min} \geqslant 1$.
Dakle tvrdnja vrijedi za svaki $m \leqslant n$.
| 19. travnja 2012. 11:45 | mljulj | Točno |
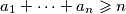 , a zatim ostatak zadatka dokazati indukcijom.
, a zatim ostatak zadatka dokazati indukcijom.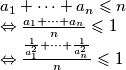
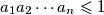
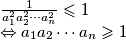
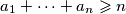

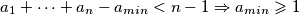 , ali i
, ali i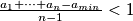 , kako aritmetička sredina nikad nije manja od svih svojih članova, znamo da postoji
, kako aritmetička sredina nikad nije manja od svih svojih članova, znamo da postoji  takav da
takav da 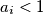 ali istovremeno i
ali istovremeno i 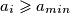 što je kontradikcija s
što je kontradikcija s 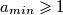 .
. 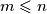 .
. 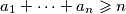 , a zatim ostatak zadatka dokazati indukcijom.
, a zatim ostatak zadatka dokazati indukcijom.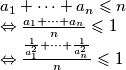
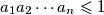
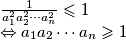
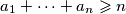

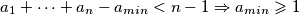 , ali i
, ali i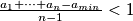 , kako aritmetička sredina nikad nije manja od svih svojih članova, znamo da postoji
, kako aritmetička sredina nikad nije manja od svih svojih članova, znamo da postoji  takav da
takav da 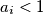 ali istovremeno i
ali istovremeno i 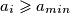 što je kontradikcija s
što je kontradikcija s 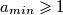 .
. 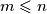 .
.  Školjka
Školjka  te
te 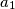 ,
, 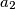 , ...,
, ..., 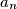 pozitivni realni brojevi za koje vrijedi
pozitivni realni brojevi za koje vrijedi 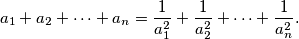
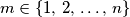 postoji
postoji  brojeva iz skupa
brojeva iz skupa 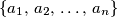 čiji je zbroj barem
čiji je zbroj barem