Točno
16. travnja 2012. 12:36 (13 godine, 9 mjeseci)
Dokažite da u svakom trokutu vrijedi nejednakost
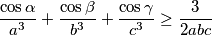
pri čemu su

duljine stranica trokuta, te
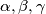
odgovarajući kutovi.
%V0
Dokažite da u svakom trokutu vrijedi nejednakost
$$\frac{\cos\alpha}{a^3} + \frac{\cos\beta}{b^3} + \frac{\cos\gamma}{c^3} \geq \frac{3}{2abc}$$
pri čemu su $a, b, c$ duljine stranica trokuta, te $\alpha, \beta, \gamma$ odgovarajući kutovi.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
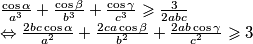
Iz kosinusovog poučka dobivamo
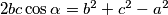
. Kada to uvrstimo dobivamo
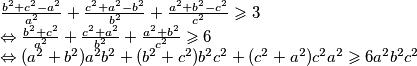
Primjenom A-G nejednakosti
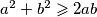
i dijeljenjem s

dobivamo
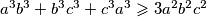
što vrijedi po A-G nejednakosti.
%V0
$\frac{\cos{\alpha}}{a^3} + \frac{\cos{\beta}}{b^3} + \frac{\cos{\gamma}}{c^3} \geqslant \frac{3}{2abc} \newline \Leftrightarrow \frac {2bc\cos{\alpha}}{a^2} + \frac {2ca\cos{\beta}}{b^2} + \frac {2ab\cos{\gamma}}{c^2} \geqslant 3$
Iz kosinusovog poučka dobivamo $2bc\cos{\alpha} = b^2 + c^2 - a^2$. Kada to uvrstimo dobivamo
$\frac{b^2+c^2-a^2}{a^2} + \frac{c^2+a^2-b^2}{b^2} + \frac{a^2+b^2-c^2}{c^2} \geqslant 3 \newline \Leftrightarrow \frac{b^2+c^2}{a^2} + \frac{c^2+a^2}{b^2} + \frac{a^2+b^2}{c^2} \geqslant 6 \newline \Leftrightarrow (a^2+b^2)a^2b^2 + (b^2+c^2)b^2c^2 + (c^2+a^2)c^2a^2 \geqslant 6a^2b^2c^2$
Primjenom A-G nejednakosti $a^2+b^2 \geqslant 2ab$ i dijeljenjem s $2$ dobivamo
$a^3b^3 + b^3c^3 + c^3a^3 \geqslant 3a^2b^2c^2$
što vrijedi po A-G nejednakosti.
| 19. travnja 2012. 11:41 | mljulj | Točno |