Točno
16. travnja 2012. 16:10 (13 godine, 11 mjeseci)
U decimalnom zapisu broj
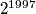
ima

znamenaka, a u zapisu broja
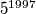
ima

znamenaka. Kolika je suma

?
%V0
U decimalnom zapisu broj $2^{1997}$ ima $m$ znamenaka, a u zapisu broja $5^{1997}$ ima $n$ znamenaka. Kolika je suma $m+n$?
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
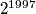
ima m znamenaka pa vrijedi:
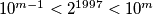
ne zavrsava na 0 pa ne vrijedi jednakost u
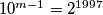
analogno vrijedi:
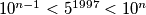
pomnozimo li ove nejednakosti dobit cemo:
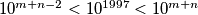
iz toga slijedi da je
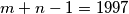
tj.
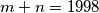
izbjegoh logaritme :D
%V0
$2^{1997}$ ima m znamenaka pa vrijedi:
$10^{m-1}<2^{1997}<10^m$
ne zavrsava na 0 pa ne vrijedi jednakost u $10^{m-1}=2^{1997}$
analogno vrijedi:
$10^{n-1}<5^{1997}<10^n$
pomnozimo li ove nejednakosti dobit cemo:
$10^{m+n-2}<10^{1997}<10^{m+n}$
iz toga slijedi da je $m+n-1=1997$ tj. $m+n=1998$
izbjegoh logaritme :D
| 16. travnja 2012. 18:25 | mgradicek | Točno |
| 16. travnja 2012. 19:08 | grga | Točno |