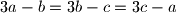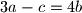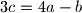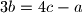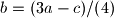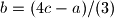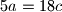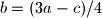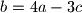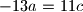Netočno
30. studenoga 2012. 19:00 (13 godine, 2 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Ocjene: (1)
Komentari:
ikicic, 1. prosinca 2012. 19:50
adnangobeljic, 1. prosinca 2012. 15:09
Ne valja ti rješenje zato što kad izjednacis 3a-b=3b-c=3c-a onda dobijes da mora da bude a=b=c a to nije moguće zato što kako bi ovi bili međusobno jednaki prije toga sva tri broja moraju biti jednaka itd. a kako su napočetku data tri različita broja ( 2009, 2012 i 2015 ) tako tvrdnja nije ostvariva.
A trebao si ionako da koristis ova tri broja sto su ti data 2009, 2012 i 2015. Kad neki uslov zadatka ne koristis znaci da ti rješenje nije tacno da znas
Pogedaj malo bliže gdje si napravio grešku u sistemu
A trebao si ionako da koristis ova tri broja sto su ti data 2009, 2012 i 2015. Kad neki uslov zadatka ne koristis znaci da ti rješenje nije tacno da znas
Pogedaj malo bliže gdje si napravio grešku u sistemu
 Školjka
Školjka 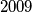 ,
, 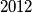 i
i 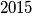 . Željko u svakom koraku označi brojeve na ploči s
. Željko u svakom koraku označi brojeve na ploči s  ,
,  i
i  u nekom poretku, a zatim ih zamjenjuje brojevima
u nekom poretku, a zatim ih zamjenjuje brojevima 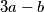 ,
, 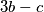 i
i 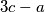 . Može li Željko uzastopnom primjenom ovog postupka postići da na ploči u nekom trenutku pišu tri jednaka broja?
. Može li Željko uzastopnom primjenom ovog postupka postići da na ploči u nekom trenutku pišu tri jednaka broja?