Točno
31. ožujka 2017. 13:53 (8 godine, 10 mjeseci)
Odredi sva realna rješenja sustava
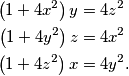
%V0
Odredi sva realna rješenja sustava
$$$\begin{align*}
\left(1+4x^2\right)y &= 4z^2\\
\left(1+4y^2\right)z &= 4x^2\\
\left(1+4z^2\right)x &= 4y^2 \text{.}
\end{align*}$$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kako je $4z^2\geq 0$ i $1+4x^2 > 0$ i $y = \frac{4z^2}{1+4x^2}$ je $y\geq 0$. Analogno $x,z\geq 0$. Ako je jedan od brojeva jednak nuli, onda su i ostali sto je jedno rjesenje $(x,y,z)=(0,0,0)$. U suprotnom $x,y,z>0$.
Kako je $(1+4x^2)y \geq 4xy$ je $4z^2 \geq 4xy$ tj. $z^2 \geq xy$, a kako je $z>0$ i $z^3 \geq xyz$, te analogno $x^3 \geq xyz$ i $y^3 \geq xyz$. Množenjem je $x^3y^3z^3\geq (xyz)^3$ pa moraju vrijediti svi uvjeti jednakosti, tj. $4x^2+1=4x$ odnosno $x=\frac{1}{2}$ te analogno $y=z=\frac{1}{2}$. Drugo i jedino preostalo rješenje je $(x,y,z)=(\frac{1}{2},\frac{1}{2},\frac{1}{2})$.