Neocijenjeno
7. travnja 2017. 22:51 (8 godine, 11 mjeseci)
Let

be a non-constant function from the set of positive integers into the set of positive integer, such that

divides
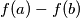
for all distinct positive integers

,

. Prove that there exist infinitely many primes

such that

divides
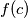
for some positive integer

.
Proposed by Juhan Aru, Estonia
%V0
Let $f$ be a non-constant function from the set of positive integers into the set of positive integer, such that $a-b$ divides $f\!\left(a\right)-f\!\left(b\right)$ for all distinct positive integers $a$, $b$. Prove that there exist infinitely many primes $p$ such that $p$ divides $f\!\left(c\right)$ for some positive integer $c$.
Proposed by Juhan Aru, Estonia
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo suprotno, da postoji svega konacno mnogo prostih djeljitelja funkcijskih vrijednosti, neka su to $ p_1, p_2, ..., p_n $, $p_i \vert f(a_i) $
Iz uvjeta onda slijedi $p_i \vert f(a_i + xp_i) $, za svaki $x$ prirodan
Dakle po kineskom teoremu ostataka postoji $a$ takav da $\prod = p_1p_2...p_n \ \vert \ f(a) $
Iz uvjeta slijedi $ \lambda = \prod f(a) \ \vert \ x \prod f(a) \ \vert \ f(a + x \prod f(a)) - f(a) $
Posto $v_{p_i} ( \lambda = \prod f(a) ) > v_{p_i}( f(a) ) $ mora vrijediti $ v_{p_i}(f(a)) = v_{p_i}(f(a + x \lambda )) $ pa onda jer $f(t)$ nema nikoje druge proste djeljitelje slijedi
$ f(a) = f(a + x \lambda) $ za svaki x prirodan
Neka je $b$ neki prirodan takav da $f(a) \neq f(b)$, onda $ a + x \lambda - b \ \vert \ f(a + x \lambda) - f(b) = f(a) - f(b) $, sto je kontradikcija za x dovoljno velik
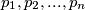 ,
, 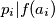
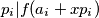 , za svaki
, za svaki  prirodan
prirodan takav da
takav da 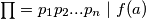
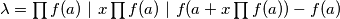
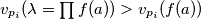 mora vrijediti
mora vrijediti 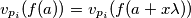 pa onda jer
pa onda jer 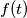 nema nikoje druge proste djeljitelje slijedi
nema nikoje druge proste djeljitelje slijedi 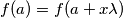 za svaki x prirodan
za svaki x prirodan neki prirodan takav da
neki prirodan takav da 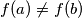 , onda
, onda 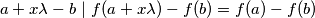 , sto je kontradikcija za x dovoljno velik
, sto je kontradikcija za x dovoljno velik  Školjka
Školjka  be a non-constant function from the set of positive integers into the set of positive integer, such that
be a non-constant function from the set of positive integers into the set of positive integer, such that  divides
divides 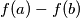 for all distinct positive integers
for all distinct positive integers  such that
such that 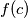 for some positive integer
for some positive integer  .
.