Neocijenjeno
7. travnja 2017. 23:49 (7 godine, 10 mjeseci)
Determine all functions
from the set of positive integers to the set of positive integers such that, for all positive integers
and
, there exists a non-degenerate triangle with sides of lengths
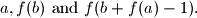
(A triangle is non-degenerate if its vertices are not collinear.)
Proposed by Bruno Le Floch, France
%V0
Determine all functions $f$ from the set of positive integers to the set of positive integers such that, for all positive integers $a$ and $b$, there exists a non-degenerate triangle with sides of lengths
$$a, f(b) \text{ and } f(b + f(a) - 1).$$
(A triangle is non-degenerate if its vertices are not collinear.)
Proposed by Bruno Le Floch, France
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
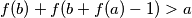za svaki prirodan, dakle je neogranicena
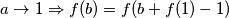, no posto je neogranicena mora vrijediti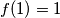 
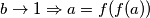
Induktivno dokazujem tvrdnju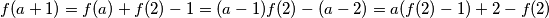 
, za svaki prirodan broj
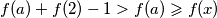za svaki 
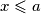, dakle 
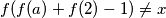za svaki 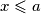, dakle 
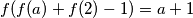, dakle 
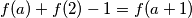, sto smo i htjeli dokazati
Posto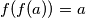 
, je bijekcija, pa 
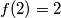, dakle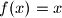 
$ f(b) + f(b + f(a) - 1) > a $ za svaki $ a $ prirodan, dakle $ f $ je neogranicena
$ a \rightarrow 1 \Rightarrow f(b) = f(b + f(1) - 1) $, no posto je $ f $ neogranicena mora vrijediti $ f(1) = 1 $
$ b \rightarrow 1 \Rightarrow a = f(f(a)) $
Induktivno dokazujem tvrdnju $ f(a+1) = f(a) + f(2) - 1 = (a-1)f(2) - (a-2) = a(f(2)-1) + 2 - f(2) $, za svaki $ a $ prirodan broj
$ b \rightarrow f(2) \Rightarrow a+1 \geqslant f(f(a)+f(2)-1) $
$ f(a) + f(2) -1 > f(a) \geqslant f(x) $ za svaki $ x \leqslant a $, dakle $ f(f(a) + f(2) - 1) \neq x $ za svaki $ x \leqslant a $, dakle $ f(f(a) + f(2) - 1) = a+1 $, dakle $ f(a) + f(2) - 1 = f(a+1) $, sto smo i htjeli dokazati
Posto $f(f(a)) = a$, $ f $ je bijekcija, pa $ f(2) = 2 $, dakle $ f(x) = x $
Školjka