 -gon, there is a fortress. At the same moment, each fortress shoots one of the two nearest fortresses and hits it. The result of the shooting is the set of the hit fortresses; we do not distinguish whether a fortress was hit once or twice. Let
-gon, there is a fortress. At the same moment, each fortress shoots one of the two nearest fortresses and hits it. The result of the shooting is the set of the hit fortresses; we do not distinguish whether a fortress was hit once or twice. Let 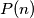 be the number of possible results of the shooting. Prove that for every positive integer
be the number of possible results of the shooting. Prove that for every positive integer 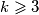 ,
, 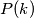 and
and 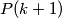 are relatively prime.
are relatively prime. Kliknite ovdje kako biste prikazali rješenje.
Koji su tocno moguci skupovi pogodaka? Skup  je skup pogodaka za neka gadjanja akko za svaki cvor bar jedan od njegovih susjeda je unutar
je skup pogodaka za neka gadjanja akko za svaki cvor bar jedan od njegovih susjeda je unutar  .
.
Smjer 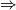 je dosta ocit iz uvjeta zadatka, dok za
je dosta ocit iz uvjeta zadatka, dok za 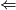 za svaki cvor biramo pucanje na sljedeci nacin:
za svaki cvor biramo pucanje na sljedeci nacin:
Ako je tocno jedan susjed u  , u njega puca.
, u njega puca.
Ako su oba susjeda u  , puca u susjeda koji je u CCW smjeru u odnosu na njega.
, puca u susjeda koji je u CCW smjeru u odnosu na njega.
Jasno je skup pogodaka podskup od  , a da svakog elementa
, a da svakog elementa  od
od  pogadjamo je jasno ako pogledamo CW susjeda od
pogadjamo je jasno ako pogledamo CW susjeda od  , on ce nuzno pucat u
, on ce nuzno pucat u  jer se nalazi na CCW strani.
jer se nalazi na CCW strani.
Zamislimo graf na cvorevima poligona, izmedju neka dva cvora postoji brid akko su udaljeni za tocno 2 u CW ili CCW smjeru. Dakle 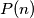 je broj skupova
je broj skupova  takvih da, ako je
takvih da, ako je 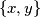 brid, onda je bar jedan od
brid, onda je bar jedan od 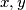 u
u  .
.
Ako je 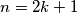 , taj graf je ciklus duljine
, taj graf je ciklus duljine 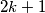 , ako je
, ako je 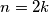 , onda je dva disjunktna ciklusa duljine
, onda je dva disjunktna ciklusa duljine  .
.
Neka je 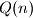 broj podskupova cvoreva od ciklusa duljine
broj podskupova cvoreva od ciklusa duljine  takvih da za svaki brid bar jedan od vrhova je u skupu.
takvih da za svaki brid bar jedan od vrhova je u skupu.
Dakle vrijedi 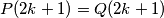 i
i 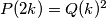
Neka je 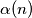 broj podskupova cvoreva lanca duljine
broj podskupova cvoreva lanca duljine  sa opet istim svojstvom kao za definiciju
sa opet istim svojstvom kao za definiciju  .
.
Fiksirajmo neki cvor  ciklusa duljine
ciklusa duljine  . On moze ili biti u skupu, ili ne. Ako je, onda je broj takvih skupova
. On moze ili biti u skupu, ili ne. Ako je, onda je broj takvih skupova 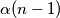 . Ako nije, onda mu susjedi nuzno moraju biti u skupu, pa je broj takvih skupova
. Ako nije, onda mu susjedi nuzno moraju biti u skupu, pa je broj takvih skupova 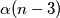 . To jest,
. To jest, 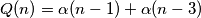
Fiksirajmo neki cvor  koji je rub lanca duljine
koji je rub lanca duljine  . Ako je u skupu, onda je broj takvih skupova
. Ako je u skupu, onda je broj takvih skupova 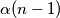 , inace
, inace 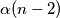 . Dakle
. Dakle 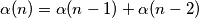
Iz 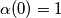 ,
, 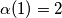 slijedi
slijedi 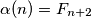 , gdje je
, gdje je 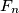
 -ti Fibonaccijev broj.
-ti Fibonaccijev broj.
Dakle 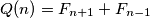
Nazad na problem, zelimo dokazati 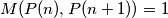
Prvi slucaj, 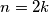
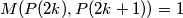
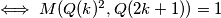
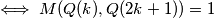
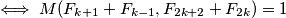
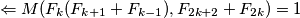
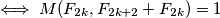
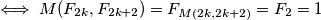
Drugi slucaj se dokazuje na isti nacin, samo cemo imati 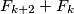 umjesto
umjesto 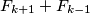
Napomena, koristeno je 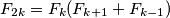 i
i 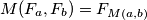
 Školjka
Školjka