Za 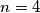 postoji, uzmimo vrhove jedinicnog kvadrata te sve vrijednosti su
postoji, uzmimo vrhove jedinicnog kvadrata te sve vrijednosti su 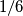
Imamo dvije moguce konfiguracije cetiri tocaka, ili cine konveksan cetverokut, ili trokut gdje je cetvrta tocka unutar tog trokuta.
Ako cine konveksan cetverokut, onda je suma suprotnih vrijednosti ista.
Ako cine trokut, onda je suma vrijednosti trokuta plus trostruka vrijednost sredisnje tocke nula.
Za 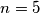 imamo 3 mogucnosti:
imamo 3 mogucnosti:
Convex hull je peterokut, redom tocke 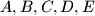 , sa vrijednostima
, sa vrijednostima 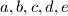
Iz  i
i 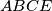 zakljucujemo
zakljucujemo 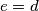 , pa simetricno su sve vrijednosti iste.
, pa simetricno su sve vrijednosti iste.
Dakle trokutevi  ,
,  i
i 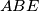 imaju istu povrsinu, dakle
imaju istu povrsinu, dakle 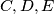 su kolinearne, kontradikcija.
su kolinearne, kontradikcija.
Convex hull je cetverokut, 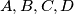 tim redom cine hull,
tim redom cine hull,  je unutar, te BSOMP
je unutar, te BSOMP  se nalazi unutar trokuteva
se nalazi unutar trokuteva  i
i 
Iz  i
i 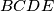 zakljucujemo
zakljucujemo  , iz
, iz  i
i 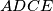 slijedi
slijedi 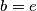
Dakle trokutevi 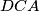 ,
, 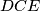 i
i 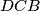 imaju istu povrsinu, dakle
imaju istu povrsinu, dakle 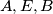 su kolinearne, kontradikcija.
su kolinearne, kontradikcija.
Convex hull je trokut, 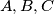 tim redom,
tim redom, 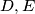 su unutar trokuta, BSOMP pravac
su unutar trokuta, BSOMP pravac  sjece duzine
sjece duzine  i
i 
Iz  i
i 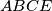 slijedi
slijedi 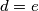
Iz 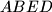 slijedi
slijedi 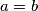
Iz 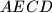 i
i  slijedi
slijedi 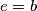
Dakle trokutevi  ,
, 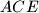 i
i 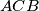 imaju istu povrsinu, dakle
imaju istu povrsinu, dakle 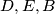 su kolinearne, kontradikcija.
su kolinearne, kontradikcija.
Za $n=4$ postoji, uzmimo vrhove jedinicnog kvadrata te sve vrijednosti su $1/6$ \\
Imamo dvije moguce konfiguracije cetiri tocaka, ili cine konveksan cetverokut, ili trokut gdje je cetvrta tocka unutar tog trokuta. \\
Ako cine konveksan cetverokut, onda je suma suprotnih vrijednosti ista. \\
Ako cine trokut, onda je suma vrijednosti trokuta plus trostruka vrijednost sredisnje tocke nula. \\
\\
Za $n=5$ imamo 3 mogucnosti: \\
Convex hull je peterokut, redom tocke $A, B, C, D, E$, sa vrijednostima $a, b, c, d, e$ \\
Iz $ABCD$ i $ABCE$ zakljucujemo $e = d$, pa simetricno su sve vrijednosti iste. \\
Dakle trokutevi $ABC$, $ABD$ i $ABE$ imaju istu povrsinu, dakle $C, D, E$ su kolinearne, kontradikcija. \\
Convex hull je cetverokut, $A, B, C, D$ tim redom cine hull, $E$ je unutar, te BSOMP $E$ se nalazi unutar trokuteva $ABC$ i $ABD$ \\
Iz $ABCD$ i $BCDE$ zakljucujemo $a = e$, iz $ABCD$ i $ADCE$ slijedi $b = e$ \\
Dakle trokutevi $DCA$, $DCE$ i $DCB$ imaju istu povrsinu, dakle $A, E, B$ su kolinearne, kontradikcija. \\
Convex hull je trokut, $A, B, C$ tim redom, $D, E$ su unutar trokuta, BSOMP pravac $DE$ sjece duzine $AC$ i $BC$ \\
Iz $ABCD$ i $ABCE$ slijedi $d = e$ \\
Iz $ABED$ slijedi $a = b$ \\
Iz $AECD$ i $ABCD$ slijedi $e = b$ \\
Dakle trokutevi $ACD$, $ACE$ i $ACB$ imaju istu povrsinu, dakle $D, E, B$ su kolinearne, kontradikcija. \\
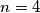 postoji, uzmimo vrhove jedinicnog kvadrata te sve vrijednosti su
postoji, uzmimo vrhove jedinicnog kvadrata te sve vrijednosti su 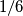
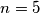 imamo 3 mogucnosti:
imamo 3 mogucnosti: 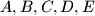 , sa vrijednostima
, sa vrijednostima 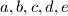
 i
i 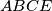 zakljucujemo
zakljucujemo 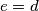 , pa simetricno su sve vrijednosti iste.
, pa simetricno su sve vrijednosti iste.  ,
,  i
i 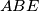 imaju istu povrsinu, dakle
imaju istu povrsinu, dakle 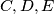 su kolinearne, kontradikcija.
su kolinearne, kontradikcija. 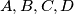 tim redom cine hull,
tim redom cine hull,  je unutar, te BSOMP
je unutar, te BSOMP  se nalazi unutar trokuteva
se nalazi unutar trokuteva  i
i 
 i
i 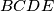 zakljucujemo
zakljucujemo  , iz
, iz  i
i 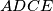 slijedi
slijedi 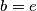
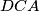 ,
, 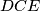 i
i 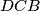 imaju istu povrsinu, dakle
imaju istu povrsinu, dakle 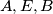 su kolinearne, kontradikcija.
su kolinearne, kontradikcija. 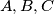 tim redom,
tim redom, 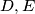 su unutar trokuta, BSOMP pravac
su unutar trokuta, BSOMP pravac  sjece duzine
sjece duzine  i
i 
 i
i 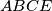 slijedi
slijedi 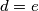
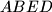 slijedi
slijedi 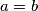
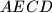 i
i  slijedi
slijedi 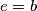
 ,
, 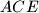 i
i 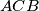 imaju istu povrsinu, dakle
imaju istu povrsinu, dakle 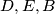 su kolinearne, kontradikcija.
su kolinearne, kontradikcija.  Školjka
Školjka 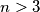 for which there exist
for which there exist  points
points 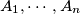 in the plane, no three collinear, and real numbers
in the plane, no three collinear, and real numbers 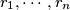 such that for
such that for 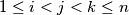 , the area of
, the area of 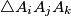 is
is 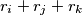 .
.