Neocijenjeno
10. travnja 2017. 01:40 (7 godine, 10 mjeseci)
Let
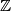
denote the set of all integers. Prove that for any integers
and
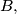
one can find an integer
for which
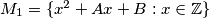
and
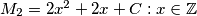
do not intersect.
%V0
Let $\mathbb{Z}$ denote the set of all integers. Prove that for any integers $A$ and $B,$ one can find an integer $C$ for which $M_1 = \{x^2 + Ax + B : x \in \mathbb{Z}\}$ and $M_2 = {2x^2 + 2x + C : x \in \mathbb{Z}}$ do not intersect.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka je $M(A, B) = \{ x^2 + Ax + B : x \in \mathbb{Z} \} $ \\
Onda vrijedi $M(A, B) = M(A-2, B-A+1) = M(A+2, A+B+1) $ \\
Dakle dovoljno je dokazati tvrdnju za $A$ jednak $0$ ili $1$ \\
Ujedno BSOMP $B=0$ jer inace samo $C$ iz $(A, 0)$ slucaja povecamo za $B$ \\
$A = 0$ \\
Neka je $C=2$, te promatrajmo oba skupa modulo $4$ \\
$x^2 \equiv 0, 1 \ (\mathrm{mod} \ 4) $ dok $2x^2 + 2x + C \equiv 2 \ (\mathrm{mod} \ 4)$ dakle skupovi su disjunktni \\
$A = 1$ \\
Neka je $C=1$, svi elementi od $M_1$ su parni, dok od $M_2$ su neparni \\
Školjka 
ili 
jer inace samo 
slucaja povecamo za 
, te promatrajmo oba skupa modulo 
dok 
dakle skupovi su disjunktni 
, svi elementi od 
su parni, dok od 
su neparni