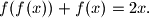Lemma 1: 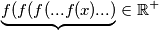
 ,
, 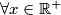 i
i 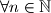 .
.
Dokaz: Zapravo je evidentno zbog čega ovo vrijedi, ako je na početku x pozitivan realan, onda je i  , pa i
, pa i  možemo uvrstiti ufunkciju itd.
možemo uvrstiti ufunkciju itd.
Lemma 2: 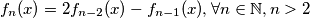
Dokaz: Prema Lemmi 1 smijemo uvrstiti umjesto  , u zadanoj jednakosti,
, u zadanoj jednakosti, 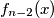 te izravno dobivamo tvrdnju Lemme 2.
te izravno dobivamo tvrdnju Lemme 2.
Lemma 1. će biti ona najvažnija, glavna značajka ovog dokaza. Naime, planiramo dokazati da je rješenje 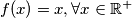 . Pretpostavimo suprotno: postoji neki
. Pretpostavimo suprotno: postoji neki 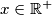 t.d.
t.d.  nije jednak
nije jednak  . Dakle, recimo
. Dakle, recimo 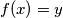 , a
, a  .
.
Promotrimo: 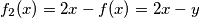 . Također, po Lemmi 2:
. Također, po Lemmi 2: 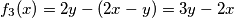 Analogno:
Analogno: 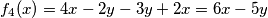 Oštro oko vještog promatrača, bez dvojbe u trenutku uočava lijepu tvrdnjicu (koja ima tendenciju postanka našom idućom lemmom):
Oštro oko vještog promatrača, bez dvojbe u trenutku uočava lijepu tvrdnjicu (koja ima tendenciju postanka našom idućom lemmom): 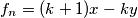 ,a parne
,a parne  , odnosno
, odnosno 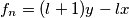 , za neparne, za neke
, za neparne, za neke 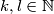
Lemma 3: Naša se intuicija ponovo pokazala izvrsnom, jer je naša "tvrdnjica" postala moćna "tvrdnjetina" koja, u obliku lemme rješava ovaj zadatak. Dakle, Lemma 3 tvrdi: 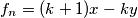 , za parne
, za parne  , odnosno
, odnosno 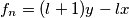 , za neparne, za neke
, za neparne, za neke 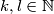
Dokaz: Dokaz provodimo dosta jakom (pretpostavljamo za n-1 i n-2) indukcijom po n. Baza: 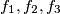 izračunati su negdje gore, i za njih vrijedi spomenuta tvrdnja.
izračunati su negdje gore, i za njih vrijedi spomenuta tvrdnja.
Slučaj 1:(parni n) Pretpostavka: 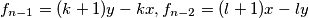 , Korak:
, Korak: 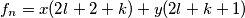 (jednostavno u Lemmu 2 uvrstimo pretpostavljene
(jednostavno u Lemmu 2 uvrstimo pretpostavljene 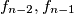 .). Trivijana jest opservacija da
.). Trivijana jest opservacija da 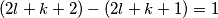 , čime smo ovaj slučaj dokazali.
, čime smo ovaj slučaj dokazali.
Slučaj 2: (neparni n) Više manje je ista stvar kao i u prošlom slučaju (samo u pretpostavku umjesto x bacimo y, i obrnuto, te pratimo i doći ćemo do tražene tvrdnje, ali da ne bi bilo da je širola lijen i da mu se nije dalo pisat, dame i gospodo, slijedi (ružno) nužno zlo):
Pretpostavka: 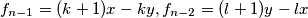 , Korak:
, Korak: 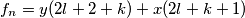 (jednostavno u Lemmu 2 uvrstimo pretpostavljene
(jednostavno u Lemmu 2 uvrstimo pretpostavljene 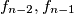 .). Trivijana jest opservacija da
.). Trivijana jest opservacija da 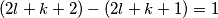 , čime smo ovaj slučaj dokazali (uopće nisam copy pasteao).
, čime smo ovaj slučaj dokazali (uopće nisam copy pasteao).
Priglupi korolar 1: 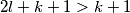 , što očito pokazuje da su koeficjenti ispred x-a i y-a strogo rastući.
, što očito pokazuje da su koeficjenti ispred x-a i y-a strogo rastući.
Sada, kada smo se oboružali lemama svih vrsta, krećemo nalemati zadatak: dakle još ranije pretpostavismo da postoji 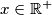 t.d.
t.d.  nije jednak
nije jednak  .
.
1. Slučaj: 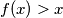 (
(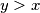 ) Neka je
) Neka je 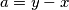 , dakle
, dakle 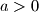 . E sad, promotrimo sve parne
. E sad, promotrimo sve parne  ove za
ove za 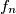 :
: 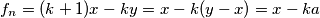 Prema Priglupom korolaru 1: k>n, to znači da ako izaberem
Prema Priglupom korolaru 1: k>n, to znači da ako izaberem 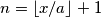 , onda će
, onda će 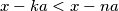 ,a za tako odfabrani
,a za tako odfabrani  , očito je
, očito je 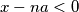 To znači, ako tako odaberem n (koji je tako odabran očito prirodan broj (x>0, a>0, 1>0) ) onda će
To znači, ako tako odaberem n (koji je tako odabran očito prirodan broj (x>0, a>0, 1>0) ) onda će 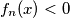 , a to ne smije biti prema Lemmi 1, pa dolazi do kontradikcije s pretpostavkom da je
, a to ne smije biti prema Lemmi 1, pa dolazi do kontradikcije s pretpostavkom da je 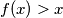 .
.
2. Slučaj, vrlo lako se kopir... također napiše: 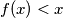 (
(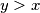 ) Neka je
) Neka je 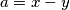 , dakle
, dakle 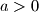 . E sad, promotrimo sve neparne
. E sad, promotrimo sve neparne  ove za
ove za 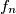 :
: 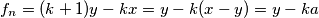 Prema Priglupom korolaru 1: k>n, to znači da ako izaberem
Prema Priglupom korolaru 1: k>n, to znači da ako izaberem 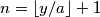 , onda će
, onda će 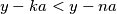 ,a za tako odfabrani
,a za tako odfabrani  , očito je
, očito je 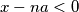 To znači, ako tako odaberem n (koji je tako odabran očito prirodan broj (y>0, a>0, 1>0) ) onda će
To znači, ako tako odaberem n (koji je tako odabran očito prirodan broj (y>0, a>0, 1>0) ) onda će 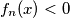 , a to ne smije biti prema Lemmi 1, pa dolazi do kontradikcije s pretpostavkom da je
, a to ne smije biti prema Lemmi 1, pa dolazi do kontradikcije s pretpostavkom da je 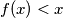 .
.
Dakle, ako pretpostavimo neki  , t.d.
, t.d.  nije jednak
nije jednak  u oba slučaja dolazi do kontradikcije s Lemmom 1, što bi po obratu po kontrapoziciji značilo da nam kontradikcija ne vrijedi, te time dobivamo da je jedino moguće
u oba slučaja dolazi do kontradikcije s Lemmom 1, što bi po obratu po kontrapoziciji značilo da nam kontradikcija ne vrijedi, te time dobivamo da je jedino moguće 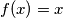 , preostaje samo provjeriti :
, preostaje samo provjeriti : 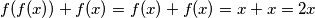
*kvadratič*
\uline{Lemma 1}: $$ \underbrace{f(f(f(...f(x)...)} \in \mathbb{R^+} $$ $$ n \quad \quad . $$, $\forall x \in \mathbb{R^+}$ i $\forall n \in \mathbb{N}$.
\uline{Dokaz}: Zapravo je evidentno zbog čega ovo vrijedi, ako je na početku x pozitivan realan, onda je i $f(x)$, pa i $f(x)$ možemo uvrstiti ufunkciju itd.
\uline{Lemma 2}: $f_n (x) =2 f_{n-2}(x)-f_{n-1}(x), \forall n \in \mathbb{N}, n>2$
\uline{Dokaz:} Prema Lemmi 1 smijemo uvrstiti umjesto $x$, u zadanoj jednakosti, $f_{n-2}(x)$ te izravno dobivamo tvrdnju Lemme 2.
Lemma 1. će biti ona najvažnija, glavna značajka ovog dokaza. Naime, planiramo dokazati da je rješenje $f(x)=x, \forall x \in \mathbb{R^+}$.
Pretpostavimo suprotno: postoji neki $x \in \mathbb{R^+}$ t.d. $f(x)$ nije jednak $x$. Dakle, recimo $f(x)=y$, a $x=x$.
Promotrimo: $f_2(x)=2x-f(x)=2x-y$.
Također, po Lemmi 2: $f_3(x)=2y-(2x-y)=3y-2x$
Analogno: $f_4(x)=4x-2y-3y+2x=6x-5y$
Oštro oko vještog promatrača, bez dvojbe u trenutku uočava lijepu tvrdnjicu (koja ima tendenciju postanka našom idućom lemmom): $f_n=(k+1)x-ky$,a parne $n$, odnosno $f_n=(l+1)y-lx$, za neparne, za neke $k,l \in \mathbb{N}$
\uline{Lemma 3}: Naša se intuicija ponovo pokazala izvrsnom, jer je naša "tvrdnjica" postala moćna "tvrdnjetina" koja, u obliku lemme rješava ovaj zadatak. Dakle, Lemma 3 tvrdi: $f_n=(k+1)x-ky$, za parne $n$, odnosno $f_n=(l+1)y-lx$, za neparne, za neke $k,l \in \mathbb{N}$
\uline{Dokaz}: Dokaz provodimo dosta jakom (pretpostavljamo za n-1 i n-2) indukcijom po n. Baza: $f_1,f_2,f_3$ izračunati su negdje gore, i za njih vrijedi spomenuta tvrdnja.
Slučaj 1:(parni n)
Pretpostavka: $f_{n-1}=(k+1)y-kx, f_{n-2}=(l+1)x-ly$, Korak: $f_n =x(2l+2+k)+y(2l+k+1)$(jednostavno u Lemmu 2 uvrstimo pretpostavljene $f_{n-2},f_{n-1}$.). Trivijana jest opservacija da $(2l+k+2)-(2l+k+1)=1$, čime smo ovaj slučaj dokazali.
Slučaj 2: (neparni n)
Više manje je ista stvar kao i u prošlom slučaju (samo u pretpostavku umjesto x bacimo y, i obrnuto, te pratimo i doći ćemo do tražene tvrdnje, ali da ne bi bilo da je širola lijen i da mu se nije dalo pisat, dame i gospodo, slijedi (ružno) nužno zlo):
Pretpostavka: $f_{n-1}=(k+1)x-ky, f_{n-2}=(l+1)y-lx$, Korak: $f_n =y(2l+2+k)+x(2l+k+1)$(jednostavno u Lemmu 2 uvrstimo pretpostavljene $f_{n-2},f_{n-1}$.). Trivijana jest opservacija da $(2l+k+2)-(2l+k+1)=1$, čime smo ovaj slučaj dokazali (uopće nisam copy pasteao).
\uline{ Priglupi korolar 1}: $2l+k+1>k+1$, što očito pokazuje da su koeficjenti ispred x-a i y-a strogo rastući.
Sada, kada smo se oboružali lemama svih vrsta, krećemo nalemati zadatak:
dakle još ranije pretpostavismo da postoji $x \in \mathbb{R^+}$ t.d. $f(x)$ nije jednak $x$.
1. Slučaj: $f(x)>x$ ($y>x$)
Neka je $a=y-x$, dakle $a>0$.
E sad, promotrimo sve parne $n$ove za $f_n$: $f_n=(k+1)x-ky=x-k(y-x)=x-ka$
Prema Priglupom korolaru 1: k>n, to znači da ako izaberem $n=\lfloor x/a \rfloor +1$, onda će $x-ka<x-na$,a za tako odfabrani $n$, očito je $x-na<0$
To znači, ako tako odaberem n (koji je tako odabran očito prirodan broj (x>0, a>0, 1>0) ) onda će $f_n (x)<0$, a to ne smije biti prema Lemmi 1, pa dolazi do kontradikcije s pretpostavkom da je $f(x)>x$.
2. Slučaj, vrlo lako se kopir... također napiše:
$f(x)<x$ ($y>x$)
Neka je $a=x-y$, dakle $a>0$.
E sad, promotrimo sve neparne $n$ove za $f_n$: $f_n=(k+1)y-kx=y-k(x-y)=y-ka$
Prema Priglupom korolaru 1: k>n, to znači da ako izaberem $n=\lfloor y/a \rfloor +1$, onda će $y-ka<y-na$,a za tako odfabrani $n$, očito je $x-na<0$
To znači, ako tako odaberem n (koji je tako odabran očito prirodan broj (y>0, a>0, 1>0) ) onda će $f_n (x)<0$, a to ne smije biti prema Lemmi 1, pa dolazi do kontradikcije s pretpostavkom da je $f(x)<x$.
$\to \gets$
Dakle, ako pretpostavimo neki $x$, t.d. $f(x)$ nije jednak $x$ u oba slučaja dolazi do kontradikcije s Lemmom 1, što bi po obratu po kontrapoziciji značilo da nam kontradikcija ne vrijedi, te time dobivamo da je jedino moguće $f(x)=x$, preostaje samo provjeriti : $f(f(x))+f(x)=f(x)+f(x)=x+x=2x$
*kvadratič*
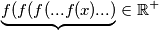
 ,
, 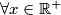 i
i 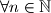 .
. , pa i
, pa i  možemo uvrstiti ufunkciju itd.
možemo uvrstiti ufunkciju itd.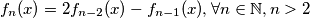
 , u zadanoj jednakosti,
, u zadanoj jednakosti, 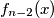 te izravno dobivamo tvrdnju Lemme 2.
te izravno dobivamo tvrdnju Lemme 2.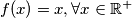 . Pretpostavimo suprotno: postoji neki
. Pretpostavimo suprotno: postoji neki 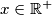 t.d.
t.d.  nije jednak
nije jednak  . Dakle, recimo
. Dakle, recimo 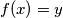 , a
, a  .
.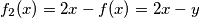 . Također, po Lemmi 2:
. Također, po Lemmi 2: 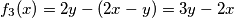 Analogno:
Analogno: 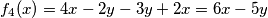 Oštro oko vještog promatrača, bez dvojbe u trenutku uočava lijepu tvrdnjicu (koja ima tendenciju postanka našom idućom lemmom):
Oštro oko vještog promatrača, bez dvojbe u trenutku uočava lijepu tvrdnjicu (koja ima tendenciju postanka našom idućom lemmom): 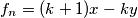 ,a parne
,a parne  , odnosno
, odnosno 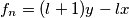 , za neparne, za neke
, za neparne, za neke 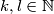
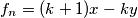 , za parne
, za parne  , odnosno
, odnosno 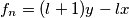 , za neparne, za neke
, za neparne, za neke 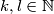
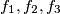 izračunati su negdje gore, i za njih vrijedi spomenuta tvrdnja.
izračunati su negdje gore, i za njih vrijedi spomenuta tvrdnja.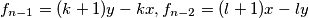 , Korak:
, Korak: 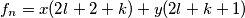 (jednostavno u Lemmu 2 uvrstimo pretpostavljene
(jednostavno u Lemmu 2 uvrstimo pretpostavljene 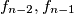 .). Trivijana jest opservacija da
.). Trivijana jest opservacija da 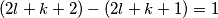 , čime smo ovaj slučaj dokazali.
, čime smo ovaj slučaj dokazali.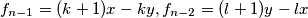 , Korak:
, Korak: 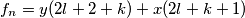 (jednostavno u Lemmu 2 uvrstimo pretpostavljene
(jednostavno u Lemmu 2 uvrstimo pretpostavljene 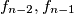 .). Trivijana jest opservacija da
.). Trivijana jest opservacija da 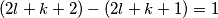 , čime smo ovaj slučaj dokazali (uopće nisam copy pasteao).
, čime smo ovaj slučaj dokazali (uopće nisam copy pasteao).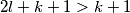 , što očito pokazuje da su koeficjenti ispred x-a i y-a strogo rastući.
, što očito pokazuje da su koeficjenti ispred x-a i y-a strogo rastući.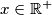 t.d.
t.d.  nije jednak
nije jednak  .
.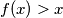 (
(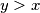 ) Neka je
) Neka je 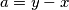 , dakle
, dakle 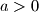 . E sad, promotrimo sve parne
. E sad, promotrimo sve parne  ove za
ove za 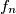 :
: 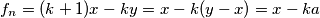 Prema Priglupom korolaru 1: k>n, to znači da ako izaberem
Prema Priglupom korolaru 1: k>n, to znači da ako izaberem 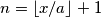 , onda će
, onda će 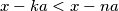 ,a za tako odfabrani
,a za tako odfabrani  , očito je
, očito je 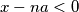 To znači, ako tako odaberem n (koji je tako odabran očito prirodan broj (x>0, a>0, 1>0) ) onda će
To znači, ako tako odaberem n (koji je tako odabran očito prirodan broj (x>0, a>0, 1>0) ) onda će 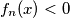 , a to ne smije biti prema Lemmi 1, pa dolazi do kontradikcije s pretpostavkom da je
, a to ne smije biti prema Lemmi 1, pa dolazi do kontradikcije s pretpostavkom da je 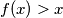 .
.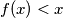 (
(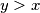 ) Neka je
) Neka je 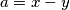 , dakle
, dakle 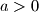 . E sad, promotrimo sve neparne
. E sad, promotrimo sve neparne  ove za
ove za 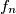 :
: 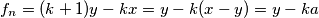 Prema Priglupom korolaru 1: k>n, to znači da ako izaberem
Prema Priglupom korolaru 1: k>n, to znači da ako izaberem 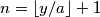 , onda će
, onda će 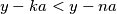 ,a za tako odfabrani
,a za tako odfabrani  , očito je
, očito je 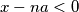 To znači, ako tako odaberem n (koji je tako odabran očito prirodan broj (y>0, a>0, 1>0) ) onda će
To znači, ako tako odaberem n (koji je tako odabran očito prirodan broj (y>0, a>0, 1>0) ) onda će 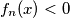 , a to ne smije biti prema Lemmi 1, pa dolazi do kontradikcije s pretpostavkom da je
, a to ne smije biti prema Lemmi 1, pa dolazi do kontradikcije s pretpostavkom da je 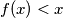 .
.
 , t.d.
, t.d.  nije jednak
nije jednak  u oba slučaja dolazi do kontradikcije s Lemmom 1, što bi po obratu po kontrapoziciji značilo da nam kontradikcija ne vrijedi, te time dobivamo da je jedino moguće
u oba slučaja dolazi do kontradikcije s Lemmom 1, što bi po obratu po kontrapoziciji značilo da nam kontradikcija ne vrijedi, te time dobivamo da je jedino moguće 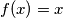 , preostaje samo provjeriti :
, preostaje samo provjeriti : 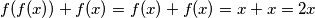
 Školjka
Školjka  takve da je
takve da je