Neocijenjeno
11. travnja 2017. 14:14 (8 godine, 10 mjeseci)
Nađite sve
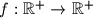
takve da je
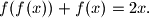
%V0
Nađite sve $f : \mathbb{R}^+ \rightarrow \mathbb{R}^+$ takve da je $$f(f(x)) + f(x) = 2x\text{.}$$
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
$$ \underbrace{f(f(f(...f(x)...)} \in \mathbb{R^+} $$ $$ \quad n \quad $$
pa uvedimo $$ a_{n}=\underbrace{f(f(f(...f(x)...)} $$ $$ \quad n \quad $$ $$ n \in \mathbb{Z}_{\geq0} $$
sada lako dobivamo rekurziju $$ a_{n+2} + a_{n+1} -2 a_{n}=0 $$
rijesavanjem rekurzije dobivamo $$ a_{n}=C_{1}+C_{2}(-2)^n $$ pa zbog $$ f(x) \in \mathbb{R^+} $$ slijedi $$a_{n}\in \mathbb{R^+} $$
ali $$ \lim_{n \to \infty} \ a_{n} <0 $$ pa zato slijedi $$ C_{2}=0 $$ sada fiksirajmo x i zelimo naci $$a_{1}=f(x)$$ ali vrijedi $$C_{1}=a_{0}=x=a_{n}=a_{1}=f(x)$$ provjerom slijedi da $$ f(x)=x$$ zaista je rijesenje zadatka