Neocijenjeno
27. srpnja 2017. 19:04 (8 godine, 6 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Označimo s  početnu nejednakost.
početnu nejednakost.
Uvrštavanjem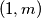 u
u  dobivamo
dobivamo
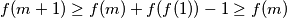
pa dobivamo da je neopadajuća.
neopadajuća.
Ideja je sada naći gornju granicu. Pretpostavimo da postoji tako da je
tako da je 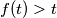 . Tada uvrštavanjem
. Tada uvrštavanjem 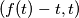 u
u  dobivamo
dobivamo
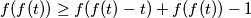
odnosno
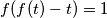
Pretpostavimo da je funkcija nekonstantna (konstanta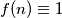 zadovoljava uvjet i daje moguću vrijednost
zadovoljava uvjet i daje moguću vrijednost  ). Tada, kako je i neopadajuća postoji tek konačan broj prirodnih
). Tada, kako je i neopadajuća postoji tek konačan broj prirodnih  takvih da je
takvih da je 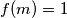 .
.
Razmotrimo onda prirodan tako da je
tako da je 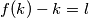 poprima najveću vrijednost. Tada uvrštavanjem
poprima najveću vrijednost. Tada uvrštavanjem 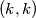 u
u  dobivamo
dobivamo
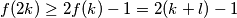
Također je po pretpostavci o maksimumu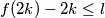 Kombiniranjem te dvije nejednakosti dobivamo
Kombiniranjem te dvije nejednakosti dobivamo 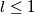 odnosno
odnosno 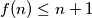 za svaki prirodan
za svaki prirodan  . Stoga
. Stoga 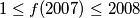 .
.
Dokazat ćemo da za svaku prirodnu vrijednost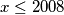 postoji funkcija
postoji funkcija 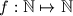 koja zadovoljava uvjet te je pritom
koja zadovoljava uvjet te je pritom 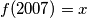 .
.
Za uzimamo konstantu
uzimamo konstantu 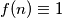 . Ona očito zadovoljava uvjete zadatka.
. Ona očito zadovoljava uvjete zadatka. 
Za ostale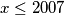 definirajmo skup
definirajmo skup 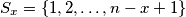 . Ako je
. Ako je 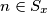 neka je
neka je 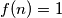 , a u suprotnom
, a u suprotnom 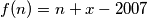 . Razmatranjem svih slučajeva se lako ustanovi da ovakve funkcije zadovoljavaju uvjet.
. Razmatranjem svih slučajeva se lako ustanovi da ovakve funkcije zadovoljavaju uvjet. 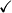 .
.
Za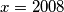 neka je
neka je 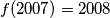 i
i 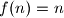 za
za 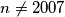 . Razmatranjem
. Razmatranjem 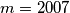 i
i 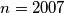 vidimo da funkcija zadovoljava uvjet, a za
vidimo da funkcija zadovoljava uvjet, a za 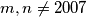 se
se  poklapa s identitetom koja je očito rješenje.
poklapa s identitetom koja je očito rješenje. 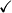
 početnu nejednakost.
početnu nejednakost.Uvrštavanjem
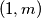 u
u  dobivamo
dobivamo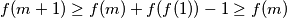
pa dobivamo da je
 neopadajuća.
neopadajuća.Ideja je sada naći gornju granicu. Pretpostavimo da postoji
 tako da je
tako da je 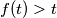 . Tada uvrštavanjem
. Tada uvrštavanjem 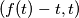 u
u  dobivamo
dobivamo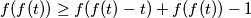
odnosno
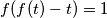
Pretpostavimo da je funkcija nekonstantna (konstanta
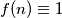 zadovoljava uvjet i daje moguću vrijednost
zadovoljava uvjet i daje moguću vrijednost  ). Tada, kako je i neopadajuća postoji tek konačan broj prirodnih
). Tada, kako je i neopadajuća postoji tek konačan broj prirodnih  takvih da je
takvih da je 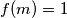 .
.Razmotrimo onda prirodan
 tako da je
tako da je 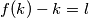 poprima najveću vrijednost. Tada uvrštavanjem
poprima najveću vrijednost. Tada uvrštavanjem 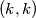 u
u  dobivamo
dobivamo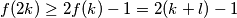
Također je po pretpostavci o maksimumu
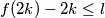 Kombiniranjem te dvije nejednakosti dobivamo
Kombiniranjem te dvije nejednakosti dobivamo 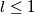 odnosno
odnosno 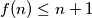 za svaki prirodan
za svaki prirodan  . Stoga
. Stoga 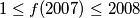 .
.Dokazat ćemo da za svaku prirodnu vrijednost
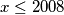 postoji funkcija
postoji funkcija 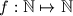 koja zadovoljava uvjet te je pritom
koja zadovoljava uvjet te je pritom 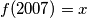 .
.Za
 uzimamo konstantu
uzimamo konstantu 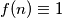 . Ona očito zadovoljava uvjete zadatka.
. Ona očito zadovoljava uvjete zadatka. 
Za ostale
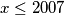 definirajmo skup
definirajmo skup 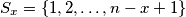 . Ako je
. Ako je 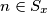 neka je
neka je 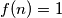 , a u suprotnom
, a u suprotnom 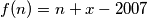 . Razmatranjem svih slučajeva se lako ustanovi da ovakve funkcije zadovoljavaju uvjet.
. Razmatranjem svih slučajeva se lako ustanovi da ovakve funkcije zadovoljavaju uvjet.  .
.Za
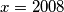 neka je
neka je 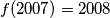 i
i 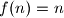 za
za 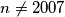 . Razmatranjem
. Razmatranjem 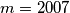 i
i 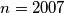 vidimo da funkcija zadovoljava uvjet, a za
vidimo da funkcija zadovoljava uvjet, a za 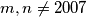 se
se  poklapa s identitetom koja je očito rješenje.
poklapa s identitetom koja je očito rješenje. 
 Školjka
Školjka 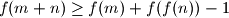
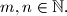 Find all possible values of
Find all possible values of